matlab2010b
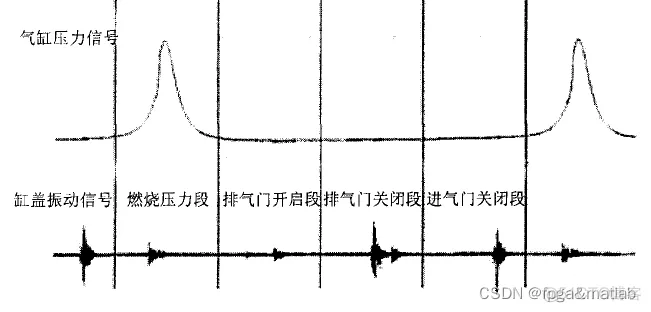
1 气缸盖压振动是多种激励力作用的结果,由于各个激励力的时间间隔性,可以通过时域加窗来提取缸盖有气缸压力引起的振动响应信号。
2 时域统计平均技术:从混有噪声干扰的信号中提取有用信号的技术。
3 平滑处理
4 等曲柄转角化和信号重采样:把振动信号也转化成横坐标是角度-360—360,纵坐标是加速度。与相应的压力信号进行对应。
5 频域分析(傅里叶):
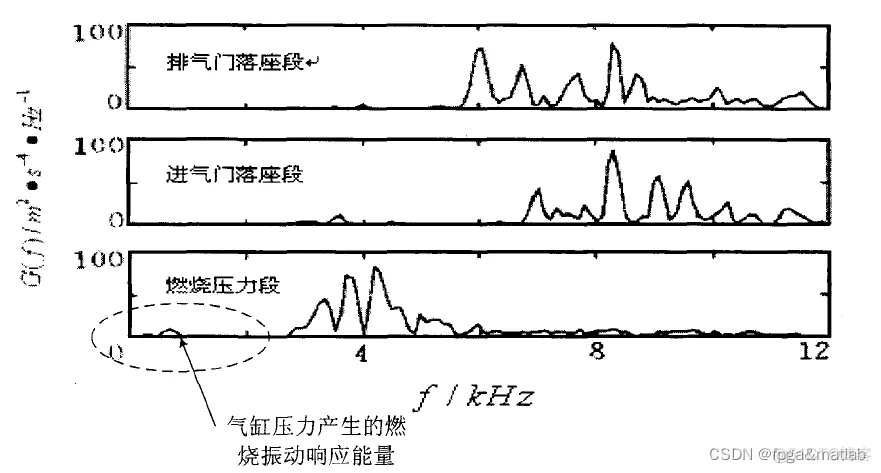
分别对他们做横坐标是频率的转化,然后看压力主要分布在哪个频率范围内。
6 低通滤波:根据上面得出的频率范围,设计滤波器,提取压力所对应的振动信号,说明为什么选用这个滤波器,滤波器的幅相频响应曲线。
7 小波分析:经小波包分解后,可以得到不同频带、不同时刻下缸盖振动响应信号的小波包系数,也就能够分析出不同激励源振动响应信号所包含的频率信息,以及不同频率下振动响应信号的能量。

| 转速/工况 | 1 | 2 | 3 | 4 | 5 |
| 1000 | 0% | 25% | 50% | 75% | |
| 1500 | 0% | 25% | 50% | 75% | 100% |
| 1800 | 0% | 25% | 50% | 75% | 100% |
网络以振动信号作为输入,压力信号作为输出。以转速为基准,一共三组,每一组以1、2、4、5工况下的数据为样本,用3(负荷50%)的数据进行测试。
原理在所给文章的的第二部分,也就是对与处理后的振动信号先进行希尔伯特分析,得到信号的幅值信息,然后根据局域波分解理论,对赋值函数进行局域波分解可得多个基本模式分量和一个趋势模式分量,而这个趋势模式分量体现了幅值函数的主要幅值信息,也是气缸压力的变化信息,称为识别压力。为了使两者具有可比性,把识别压力波形的单位和最大值归化为实测压力的单位和最大值。
clc;clear;close all;warning off;addpath 'func\'%针对不同采样率的信号可能需要你手动调整的一些参数%针对不同采样率的信号可能需要你手动调整的一些参数%******加窗的长度******************************************N = 512;%******时域统计平均技术的采样次数***************************K = 16;%1000:10 , 10 , 10 , 35%1500:10 , 12 , 12 , 11 , 10%1800:10 , 13 , 16 , 16 , 16%******平滑宽度********************************************LL = 3; flag = 0;%是否需要平滑,个人觉得这里不进行平滑效果更好%******压力点判决门限***************************************KK = 5.5;%1000:5.5 , 6.5 , 6.5 , 5%1500:6 , 9 , 9 , 6 , 6%1800:5.5 , 7 , 7 , 5.5 , 5.5%******选择第几段信号***************************************NO_ = 20;%******滤波器的截止频率和采样频率的倍数**********************SS = 32;%******设置信号采样率***************************************Fs = 1000;%%%调用信号%调用信号%调用压力信号Preasure = xlsread('EXCELer\pressure\p1800-100.xls','Sheet1','A3:B722'); %调用振动信号vibration = xlsread('EXCELer\vibration\v1800-100.xls','Simulated Signal','A1:A65535'); %%%调用预处理函数y = func_signal_process(N,K,LL,KK,NO_,SS,Fs,Preasure,vibration); figure;plot(y);title('预处理之后截取的信号');%%%%传递函数法进行识别L = length(y);NFFT = 2^nextpow2(L); y2 = fft(y,NFFT);f = Fs/2*linspace(0,1,NFFT/2+1); P = Preasure(:,2)';L = length(P);NFFT = 2^nextpow2(L); P2 = fft(P,NFFT);f = Fs/2*linspace(0,1,NFFT/2+1);%计算传递函数H = y2./P2;%计算H的幅值和相位magH= abs(H); %信号的幅值 angH= angle(H); %信号的相位 f = Fs/2*linspace(0,1,NFFT/2+1);figure;subplot(211);plot(f,magH(1:length(f)));title('信号幅值'); subplot(212);plot(f,angH(1:length(f)));title('信号相位'); %下面是根据构造的H,对任意几个振动信号进行识别,这里选择了任意的2个进行识别%下面是根据构造的H,对任意几个振动信号进行识别,这里选择了任意的2个进行识别%%%根据计算得到的H,对其他的压力信号进行识别%根据计算得到的H,对其他的压力信号进行识别%根据计算得到的H,对其他的压力信号进行识别%根据计算得到的H,对其他的压力信号进行识别y_sb1 = func_signal_process(N,K,LL,KK,19,SS,Fs,Preasure,vibration);L = length(y_sb1);NFFT = 2^nextpow2(L); y2_sb1 = fft(y_sb1,NFFT); %识别压力为:Psb = y2_sb1./(H);%IFFT变换,恢复出压力信号P_real = ifft(Psb,NFFT);figure;KER = 360;plot(-KER+1:KER,P,'r');title('实际测试信号');hold onplot(-KER+1:KER,P_real(1:length(P)),'b--');title('识别信号');hold onlegend('实际测试信号','识别信号'); %%%根据计算得到的H,对其他的压力信号进行识别%根据计算得到的H,对其他的压力信号进行识别%根据计算得到的H,对其他的压力信号进行识别%根据计算得到的H,对其他的压力信号进行识别y_sb1 = func_signal_process(N,K,LL,KK,12,SS,Fs,Preasure,vibration);L = length(y_sb1);NFFT = 2^nextpow2(L); y2_sb1 = fft(y_sb1,NFFT); %识别压力为:Psb = y2_sb1./(H);%IFFT变换,恢复出压力信号P_real = ifft(Psb,NFFT);figure;KER = 360;plot(-KER+1:KER,P,'r');title('实际测试信号');hold onplot(-KER+1:KER,P_real(1:length(P)),'b--');title('识别信号');hold onlegend('实际测试信号','识别信号');1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77.78.79.80.81.82.83.84.85.86.87.88.89.90.91.92.93.94.95.96.97.98.99.100.101.102.103.104.105.106.107.108.109.110.111.112.113.114.115.116.117.118.119.120.121.122.123.124.125.126.127.128.129.130.131.132.133.134.135.136.137.138.139.140.141.
原始提取的信号
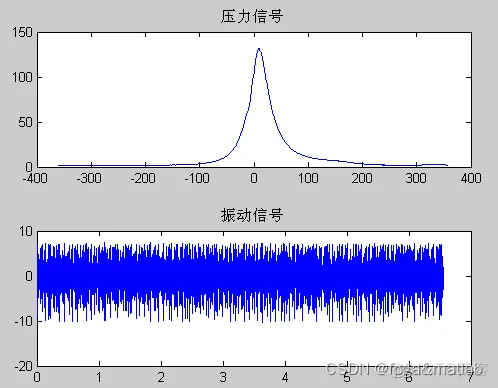
加窗处理,这里使用的是hamming窗
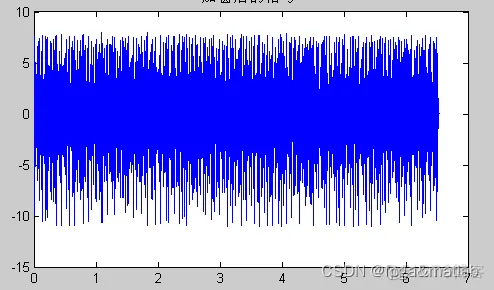
时域平均统计处理
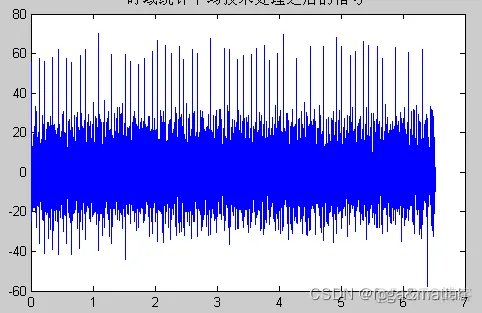
时域平均统计处理之后,平滑之后的处理
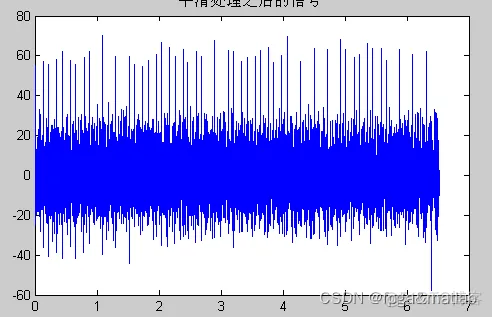
截取的信号,FFT变化之后,滤波后的信号,以及滤波之后的频谱信号
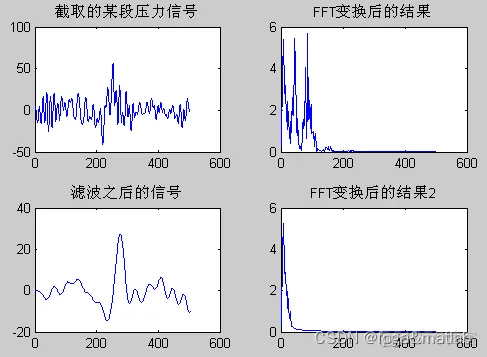
小波变化之后的频谱分析:
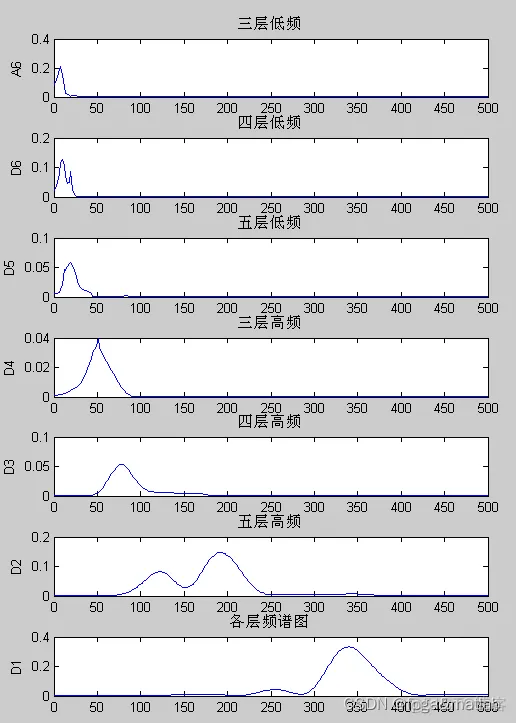
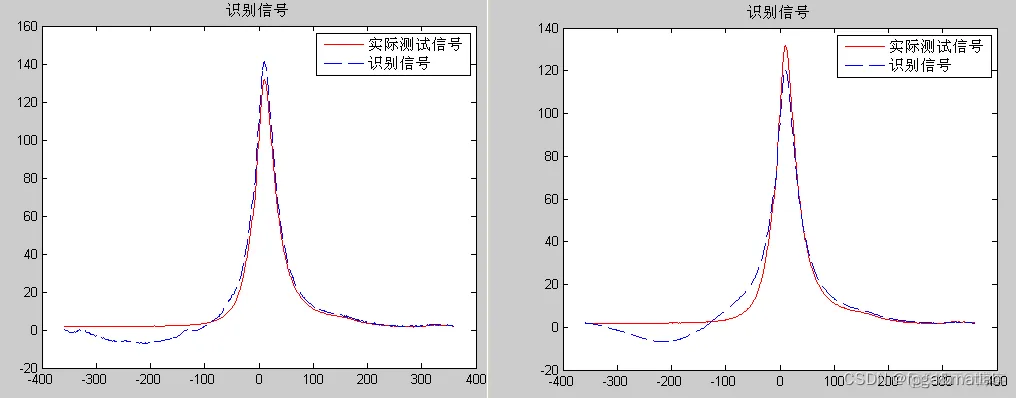
我们最后得到的仿真结果如下所示:
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删