MATLAB的汽车操纵稳定性仿真分析

0 引言

随着道路的改善，特别是高速公路的发展，汽车以100km/h或更高车速行驶的情况是常见的。现代轿车设计的最高车速一般常超过200km/h，有的运动型轿车甚至超过300km/h。因此，汽车的操纵稳定性日益受到重视，成为现代汽车的重要使用性能之一。

1 前轮转向车辆的操纵性能计算机模型

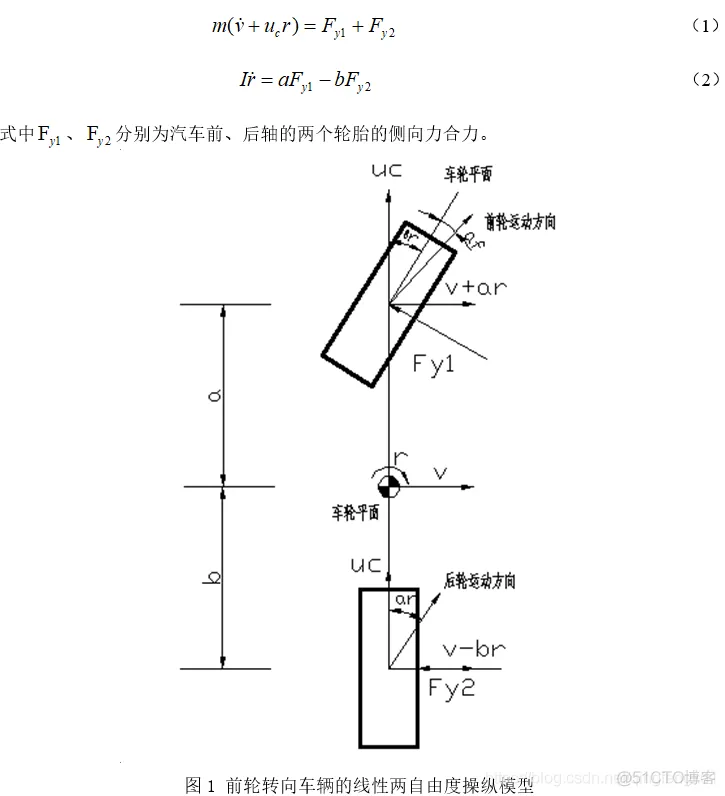
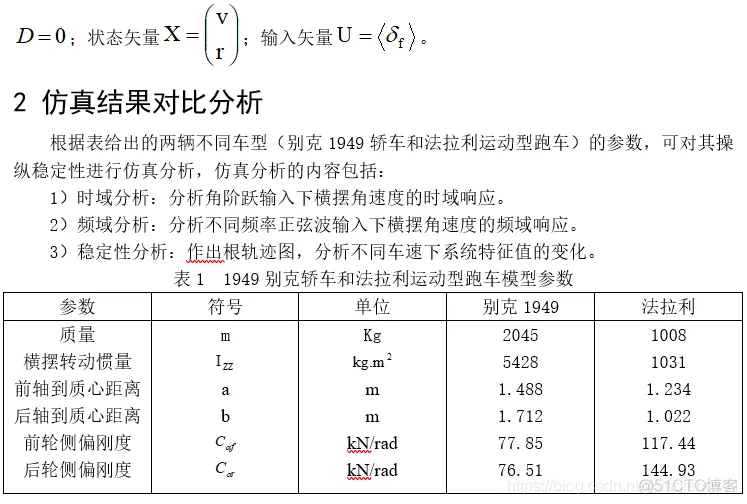
汽车以恒速行驶时，汽车只有沿y轴的侧向远动与绕z轴的横摆运动两个自由度。此外，汽车的侧向加速度限定在0.4g以内，轮胎侧偏特性处于线性范围。图1所示为一个由前后两个侧向弹性的轮胎支撑于地面、具有侧向及横摆运动的线性二自由度汽车模型，其运动方程为：

2.3 稳定性分析

通常，随着车速的提高，车辆的行驶稳定性下降。对具有过多转向特性的车辆而言，当车速超过其极限车速时，系统将处于不稳定工况，即意味着在很小的干扰输入时，系统将产生很大的响应输出（如高速转向时车辆可能发生侧滑）。而车辆行驶的稳定性与其等效线性系统的特征值有密切的联系。

在MATLAB环境中有多种方法可以求系统的特征根（即极点），其中最直接的方法可调用eig（）命令来求一个矩阵的特征值。由控制理论可知，一个可观、可控的线性系统的就是状态矩阵A的特征值，因此，求解车辆在不同车速（15~60m/s范围内）的特征根，同时在同一复平面中作图，可采用如下MATLAB程序段：

登录后复制

U=15：5：60；

for j=1：length(U)

A=[-(Cf+Cr)/(M*U(j)) -(a*Cf-b*Cr)/(M*U(j))-U(j)

-(a*Cf-b*Cr)/(Iz*U(j)) -(a^2*Cf+b^2*Cr)/(Iz*U(j))]；

plot(real(eig(A))，imag(eig(A))，'bx')；

hold on；

end

其中，命令语句real（）和imag（）分别用于系统特征值的实部和虚部求解。

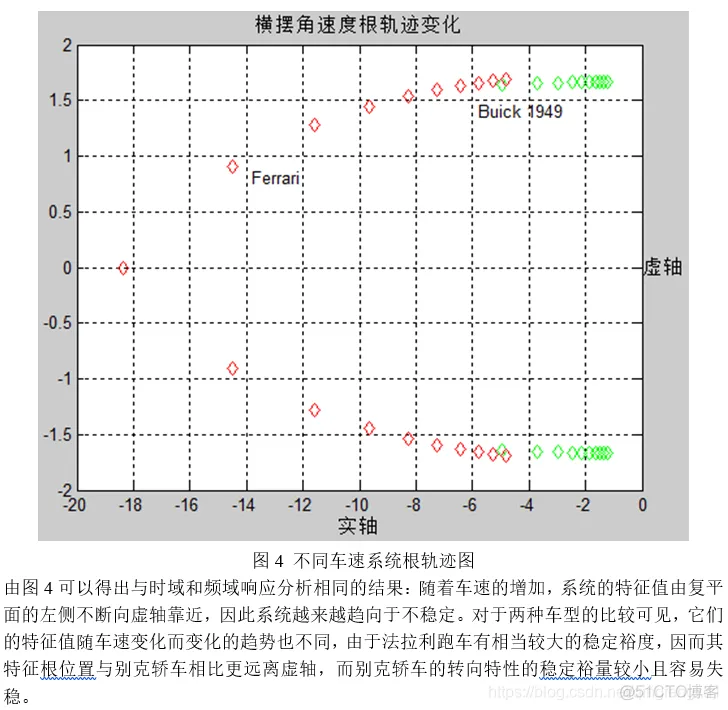
不同车速下的根轨迹变化如图4所示。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删