FLUENT中存在很多种压力,包括参考压力pref,绝对压力Pabs,相对压力Prel ,表压pgauge,总压 ptotal,动压pdynamic ,静压 pstatic,大气压patm 等。这里以一个实例来说明这些压力关系。
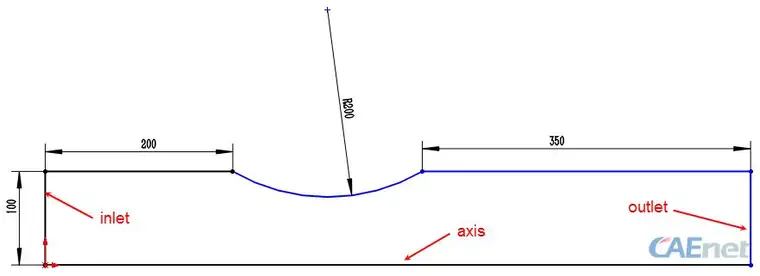
图 1几何模型
这些压力之间的关系:

1、计算条件
计算模型为旋转轴对称模型,半径100mm。

图 2计算网格
计算用网格如图2所示。流体密度1000kg/m3,粘度0.001Pa.s, 雷诺数2e5,选择Realizable k-epsilon模型,增强壁面函数模型。
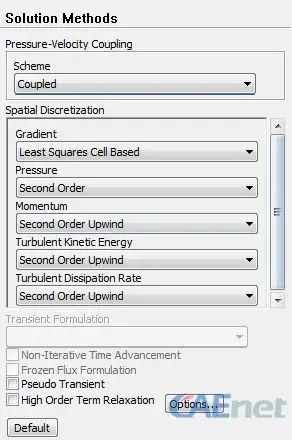
图 3求解方法
求解方程使用Coupled,其他方程使用二阶格式以提高精度。设置残差标准1e-6。
2、结果分析
计算条件:入口采用速度入口,速度1m/s,出口使用outflow ,参考压力设置为101325。
静压分布与速度分布云图分布如图4、图5所示。动压分布如图6所示。
从上述三幅图可以看出一下关系:(1)速度分布趋势与动压分布趋势保持一致,即速度大的区域,动压也较大(2)静压分布于速度分布呈相反趋势,即静压大的区域速度较小。
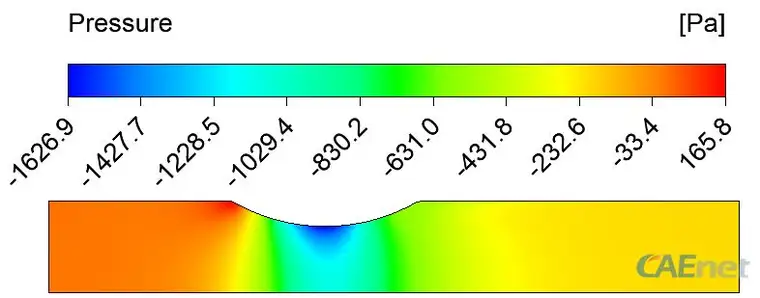
图 4静压分布
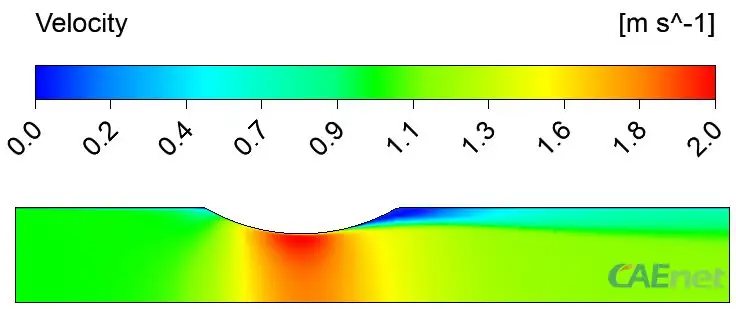
图 5 速度分布
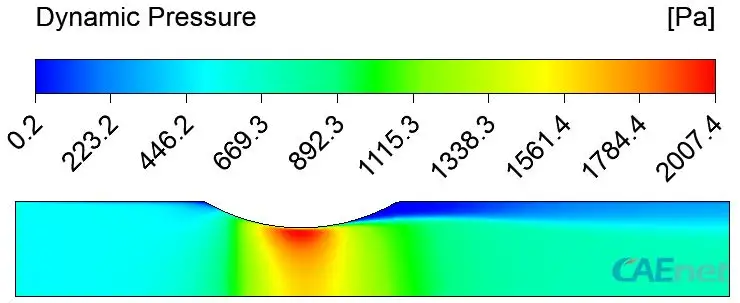
图 6 动压分布
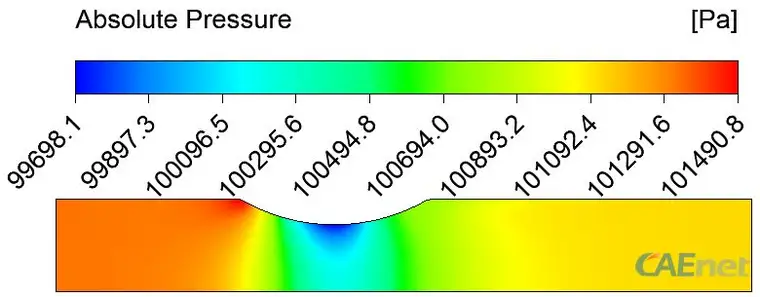
图 7绝对压力
图7为绝对压力分布,其分布趋势与图4所示的静压分布趋势完全一致,所不同的只是物理量大小,它们的值相差101325,即所设置的参考压力。下面以axis边界上物理量进行研究。
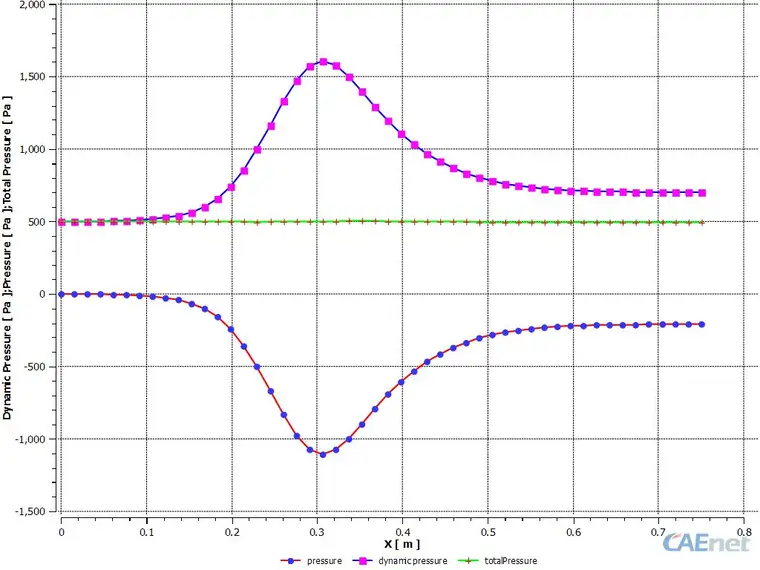
图 8 axis边界压力关系曲线
图8为axis边界上静压、动压及总压关系,很明显的可以看出,总压=静压+动压。
新建一个变量PressureSum,其表达式为Dynamic Pressure+Pressure,观察其与totoalPressure的区别。如图9所示,两物理量的值基本保持一致。

图 9总压与自定义压力曲线
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删