产品
双折射材料和波片
常用大多数波片利用的是材料的双折射特性。双折射即材料的折射率取决于光的偏振方向和传播方向。双折射材料有很多种类型，然而单轴晶体型材料通常用于波片。单轴晶体有两个相互垂直的固定折射率轴，其中一个是晶体光轴。通常光波由两个偏振分量组成，这两个偏振分量受不同的等效折射率控制。
其中快轴平行于晶体光轴的方向 ，慢轴则与快轴正交。
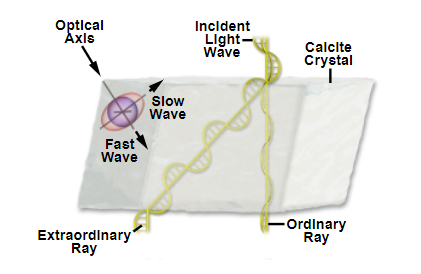
图 1. 双折射材料以及光线路径
(https://www.microscopyu.com/techniques/polarized-light/principles-of-birefringence )
这两个方向称为“快轴”和“慢轴”，其折射率值称为寻常光折射率和非寻常光折射率。光沿快轴方向的折射率低，且光沿快轴方向的相速度比其慢轴方向快。
一般来说，完全偏振光可以视为由两个偏振分量组成。两个偏振分量受不同的等效折射率控制。由于材料和偏振特性，入射偏振光在通过材料传播时被分成快轴或慢轴两个偏振分量。
在制作波片时，需要将双折射材料被切割成板状，同时要选择切割方向，使晶体光轴平行于板的表面。
例如，我们考虑以与快轴成 45 度角入射波片的垂直方向的线偏振光。光波通过波片后，将被分成“快”轴和“慢”轴两个偏振分量。这两个偏振分量以不同的速率进行相位累加，它们之间的相位差称为“相位延迟”， 如图 2 所示。
这就是双折射波片的基本原理。
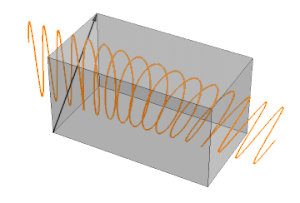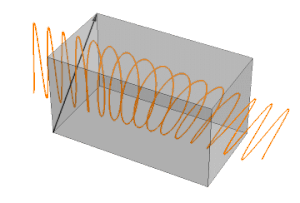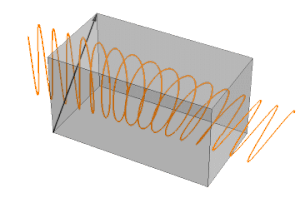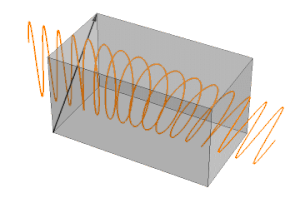
图 2. 双折射半波片中的偏振图像
(https://en.wikipedia.org/wiki/Waveplate#Quarter-wave_plate)
设计单色四分之一波片
在设计单色波片之前，理解上述理论十分重要。
例如，四分之一波片将在光的两个偏振分量之间引入四分之一波长相位延迟。要设计四分之一波片的话，我们可以使用如下公式来计算平行平板的厚度 t。
(m+14)∗λ=t∗(ne(λ)−no(λ))(m+14)∗λ=t∗(ne(λ)−no(λ))
其中：
OpticStudio的“双折射”材料目录中包含一些常用的双折射材料。要使用该材料目录的话，请在系统选项的“材料目录”选项卡中选择相关目录，如图 3 所示。
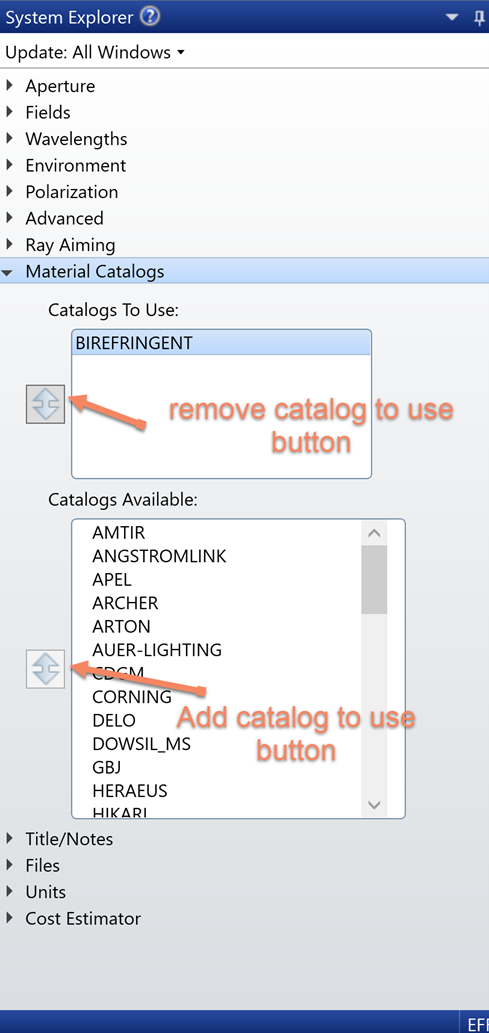
图 3: 系统选项中的材料目录选项卡
现在，我们以使用 QUARTZ 材料为例，这种材料一般是指结晶的氧化硅，且被称为“晶体”。“快”轴方向在“QUARTZ”材料中定义，“慢”轴方向在“QUARTZ‑E”材料中定义。同时我们可以在 OpticStudio 的色散图中检查对应折射率。
图 4. OpticStudio 中的色散图
此功能提供了折射率与波长的关系列表和图表，如图 5 所示。
图 5. “QUARTZ” 以及 “QUARTZ-E” 材料的折射率色散图
将 Glass 1 设置为 QUARTZ，将 Glass 2 设置为 QUARTZ-E 以查看图表值，如图 5 所示。
此时，no =1.5487281 和 ne = 1.579932，波长为 0.5 μm。
石英板的最小厚度可以使用前面的公式计算得出厚度 t = 13.491 µm。
单色四分之一波片建模
现在，我们在 OpticStudio 中模拟如上波片。在附件中可以找到一个名为 “Monochromatic wave‑plate.ZAR” 的示例文件。
材质为 “QUARTZ”，晶体光轴沿 X 轴方向，光线传播方向沿 Z 轴。在此文件中波长设定为 0.5 µm。
首先，我们要设置入射光线的偏振态。在 “System Explorer” 的 “Polarization” 选项卡中，取消选中 “Unpolarized” 并将偏振态设置为右旋圆偏振光，如图 6 所示。
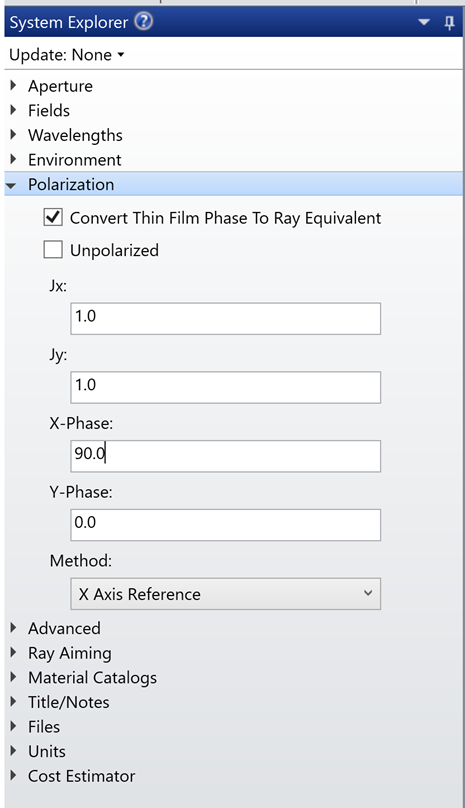
图 6. 系统选项中的偏振设置
“X‑Phase” 是琼斯矢量的相位角，以度为单位。它表示 X 方向电矢量波阵面的相位延迟。如果观察者转身观察入射光线，观察者首先会看到沿 Y 方向的电矢量振幅，然后是沿 X 方向的电矢量振幅。
因为电场的能量（电矢量振幅）对于观察者而言是顺时针旋转的，所以这种偏振态被称为“右手圆偏振”。请注意，为了在 OpticStudio 中表示完全圆偏振，“Jx” 和 “Jy” 的值必须相同且具有 90 度相位差。
我们可以使用 OpticStudio 中的 “Birefringent In” 和 “Birefringent Out” 表面对来双折射材料进行建模。“Birefringent In” 表面有一些重要参数需要设定，即 X、Y、Z 余弦参数和模式参数。
图 7. 帮助文件中“Biregringent In”对于模式 2 和模式 3 的说明
我们将模式设定为 2 或 3。
现在入射光线为右旋圆偏振光，并且定义偏振光的 X 方向有 90 度的相位延迟。一个最薄的单色波片可以被设计成快轴方向平行于 X 方向。为此，在第 1 表面之后插入第 2 表面，并将第 2 个表面设置为 “Biregringent In”，将第3个表面设置为 “Biregringent Out”。
其余的大部分设置都是默认配置。孔径类型为入瞳直径，孔径直径为 0.1。 波长 1 为 “0.5”。
图 8 显示了如上条件下的镜头数据编辑器、3D 布局和偏振光瞳图。
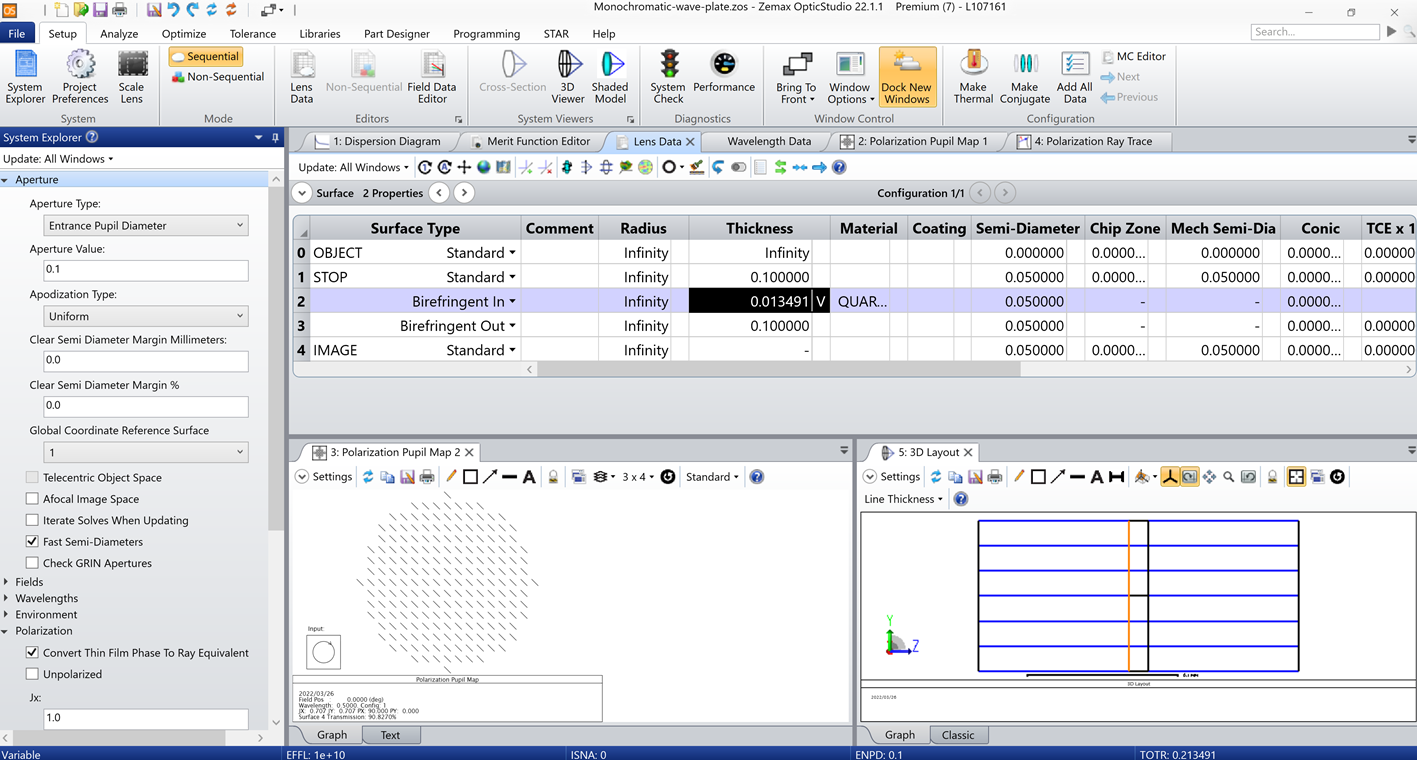图 8. OpticStudio 中的示例模型
根据偏振光瞳图所示，右旋圆偏振光变为线偏振光。这一结果可以使用评价函数中的 CODA 操作数来确认。
帮助文件中有关于 CODA 操作数的详细描述。 CODA可以计算出光线的延迟，相位差。
图 9. 帮助文件中 CODA 操作数的解释说明
图 10 展示的是评价函数的值，其结果大致为 0，符合预期。
此处加一注释。波片的厚度可以在计算值的基础上再度优化。对此，我们可以将 CODA 操作数的权重更改为 1，并将表面 2 的厚度设置为变量。
通用图表的另一功能是可以使用 Universal Plot 1D 观察延迟随第二表面厚度的变化情况。
图 10. “评价函数”和“通用图表”的结果
在图 10 中，CODA操作数返回至介于 -π 至 π 之间。
接下来，让我们考虑如何计算由波片产生的光程差。OpticStudio 有一个 OPTH 操作数来计算光程。OPTH 可以计算表面的光程。然而，每个表面都需要具有各向同性/均匀的材料。
因此，在这种情况下，多配置编辑器可用于将 “Birefringent In” 和 “Birefringent Out” 表面更改为 “标准” 表面以及对应表面的材料。在示例文件中，结构 2 的材料是 “QUARTZ”，结构 3 的材料是“QUARTZ‑E”。由于没有用于更改表面类型的多重配置操作数，因此使用 “IGNR” 多重结构操作数来忽略原始表面。
图 11. 多重结构编辑器、通用图表和评价函数
在多重结构编辑器中，Configuration 1 为波片结构。Configuration 2 使用寻常折射率计算相位， Configuration 3 使用非寻常折射率计算相位。
在评价函数编辑器中，CONF 操作数用于更改结构，OPTH 操作数用于计算相位。接下来解读评价函数：
最后：
要计算延迟，需要在评价函数中将第 3 行的权重设置为 1.0，并将第 17 行的权重设置为 0.0。
要计算波片中的光程差，需要在评价函数中将第 3 行的权重设置为 0.0，并将第 17 行的权重设置为 1.0。
建模消色差四分之一波片
现在，让我们为宽带光源建模消色差波片。在附件中可以找到一个名为 “Achromatic‑wave‑plate.ZAR” 的示例文件。消色差波片可以被视为与消色差透镜功能相同，即两个或多个不同材料的波片组合起来可以抵消色散。比如以下网站：https://www.thorlabs.com/newgrouppage9.cfm? objectgroup_id=854
列举 “石英” 和 “氟化镁” 作为消色差波片的材料。OpticStudio 的双折射材料目录中包含了 “QUARTZ” 和 “MgF2”。
该模型将包含两组使用以上材料建模的 “Birefringent In” 和 “Birefringent Out” 表面。两组双折射材料的晶体光轴都是正交的。例如，如果前波片的晶体光轴为 X 方向，则后波片的晶体光轴将为 Y 方向。这是为了有效利用色散效应。
示例文件模拟了一个 0.5 到 0.7 µm 的消色差四分之一波片。与之前的模型一样，入射光线为右旋圆偏振光，如图12所示。
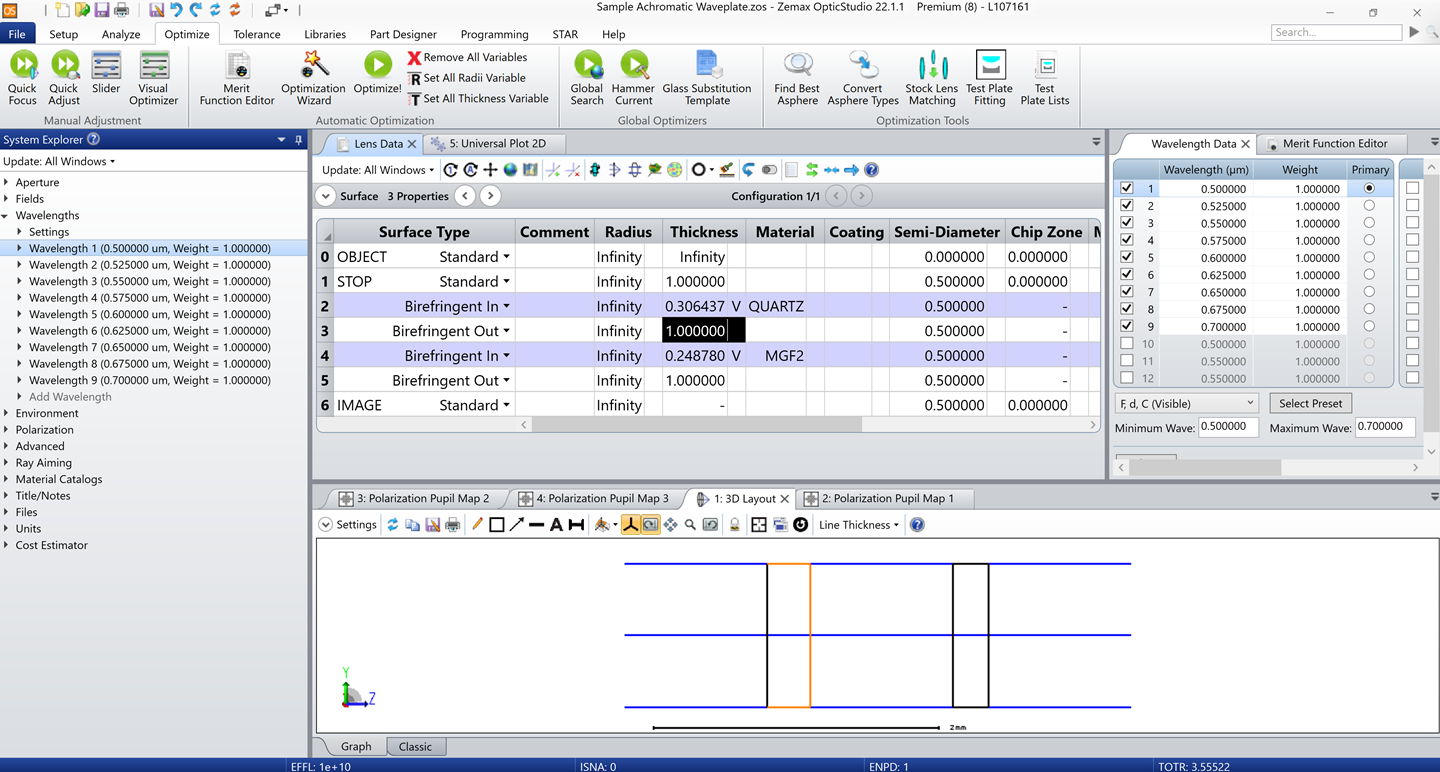
图12. 消色差波片模型
系统布局如图 12 所示。与图 8 相比，此处多了一组 “Birefringent In” 和 “Birefringent Out” 面。通过这一系列波片的光波在 X 和 Y 方向上传播的光程可以通过如下公式计算：
X(λ):n1o(λ)t1+n2e(λ)t2X(λ):n1o(λ)t1+n2e(λ)t2
Y(λ):n1e(λ)t1+n2o(λ)t2Y(λ):n1e(λ)t1+n2o(λ)t2
其中：
由于在上述方程中折射率是波长的函数，因此可以通过优化计算得出具有最小色散的波片的厚度。
“CODA” 操作数可用于计算不同波长光的相位延迟。设计该系统的评价函数等价于延迟的平方和。
我们可以使用 TTHI 操作数来控制波片的厚度。优化评价函数即使如下公式得到最小值。
∑ni=0(X(λn)+0.25λn−Y(λn))2∑i=0n(X(λn)+0.25λn−Y(λn))2
为了找到一个好的解决方案，需要使用 “Hammer Current Optimization”，因为它会避免局部最小值。需要将表面 2 和表面 4 的厚度设置为变量。优化后的结果如图 13 所示。
图 13. 优化后的结果
根据图 13，评价函数接近于 0，偏振光瞳图显示了圆偏振光通过波片后变为线偏振光。
现在可以使用 Universal Plot 2D 检查两个波片的厚度与相位延迟之间的关系。
为此，需要将 TTHI 操作数的权重更改为 0，因为该操作数与延迟无关。结果如图 14 所示。
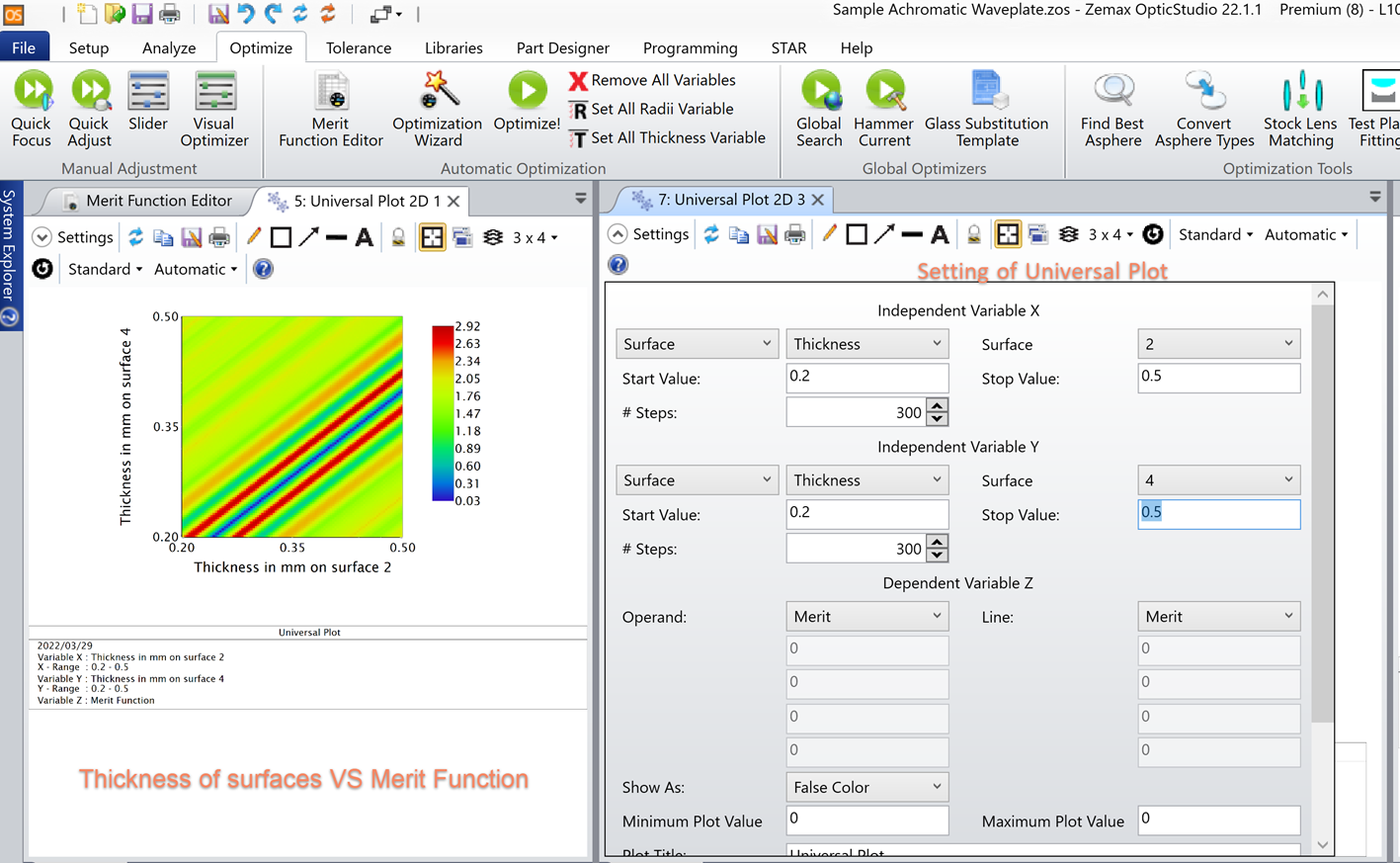
图 14. 评价函数的通用图
根据绘图，当厚度差恒定时，相位延迟似乎最小。
这表明两个波片之间的差异相比于波片的整体厚度，对消色差波片性能的影响更为重要。在
图 15 中，更改厚度比例以更清楚地显示最佳厚度范围。
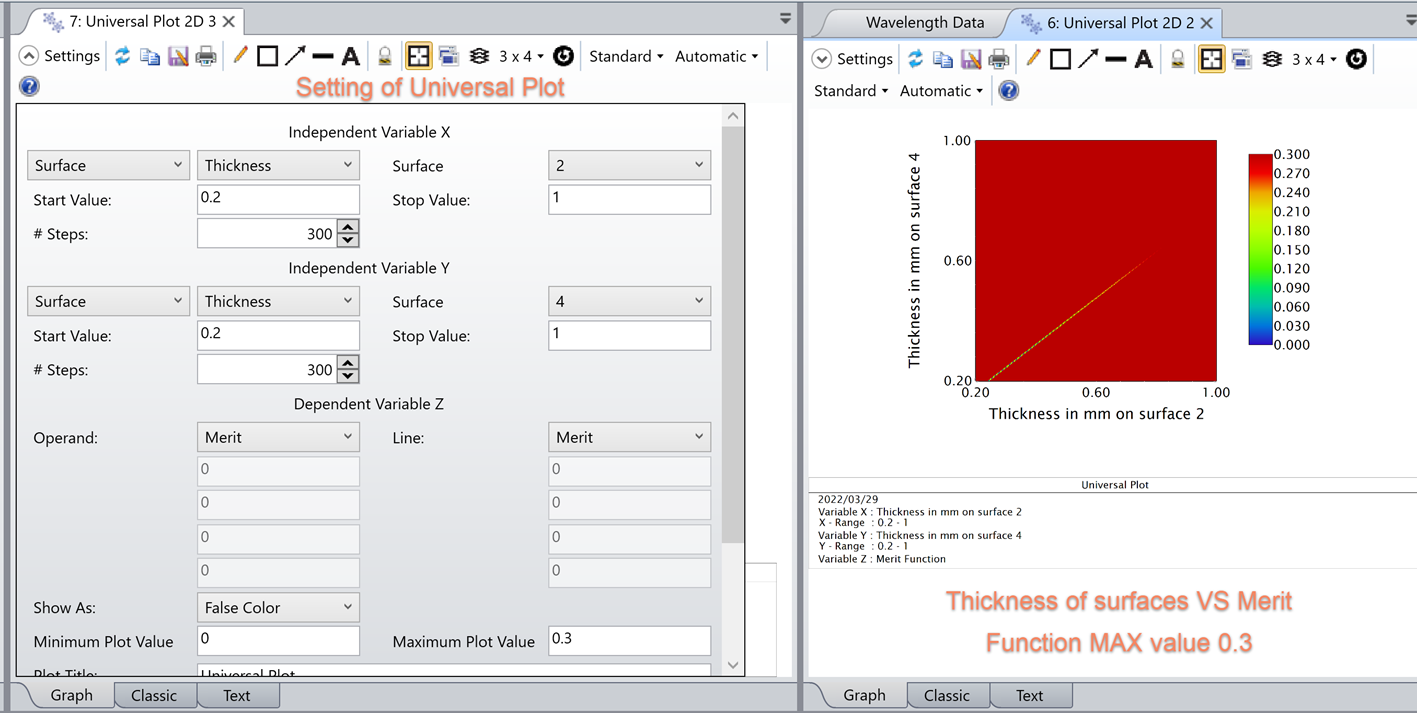
总结
本文介绍如何在 OpticStudio 中建模和设计真正的波片。设计波片后，可以使用 “通用绘图” 中的评价函数评估其性能。
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删
155-2731-8020
