Ansys Lumerical CMOS光学仿真方法

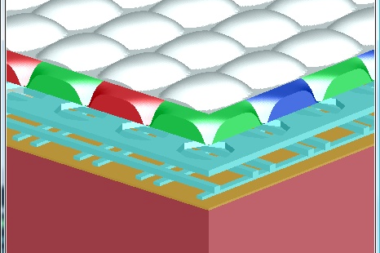
通过使用更小的像素尺寸和更大的填充因子，基于CMOS图像传感器像素的数码相机系统的成本正在降低。但是，只有在不牺牲图像质量的情况下，CMOS像素尺寸减小才是可以接受的。随着CMOS像素尺寸的不断减小，图像信噪比降低，相邻传感器像素之间的串扰也随之增加。这些效应可以通过计算机仿真的仔细设计优化来抵消，在当前像素尺寸下，计算机仿真需要麦克斯韦方程组的全矢量解。

在本主题中，我们将讨论CMOS图像传感器的趋势，对仿真的影响，可以仿真的结果类型，并描述实现这些目标的完整仿真方法。

波动光学和射线光学

当我们接近波长尺度结构时，我们对较大结构提出的许多典型问题不再有意义。例如，如果我们在特定位置在Si中产生电子空穴，我们可能想知道光子在被吸收之前通过哪个微透镜。在波动光学中，这个问题无法回答，因为光子是一种波，穿过所有微透镜，它在特定位置被吸收的概率取决于它与自身产生的干涉图案。如果我们阻挡其中一条路径，例如通过覆盖一个透镜，我们将修改干涉图案。实际上，光子采用所有可能的路径，并且必须包含所有路径才能获得正确的结果。只有在更大的长度尺度上，我们才能忽略这些多路径干扰效应。

我们可能想问光子在被吸收之前走的是哪条路。

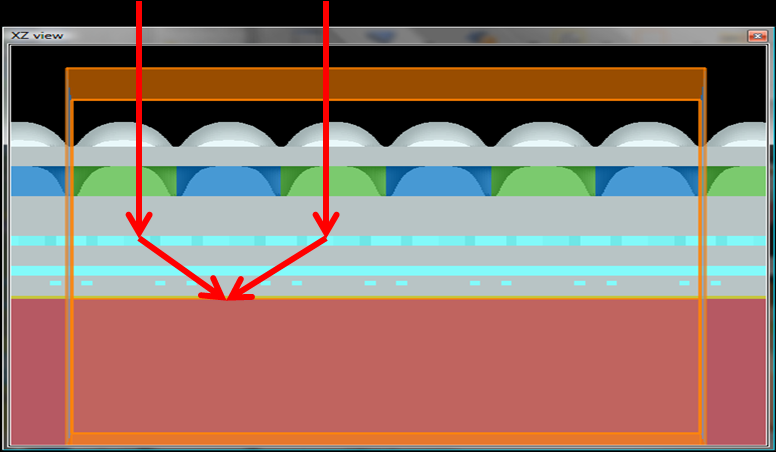
在波长尺度上，每个光子都会产生复杂的干涉图案，从而决定Si中吸收的概率。如果不修改干涉图样，就不可能确定一条特定路径。

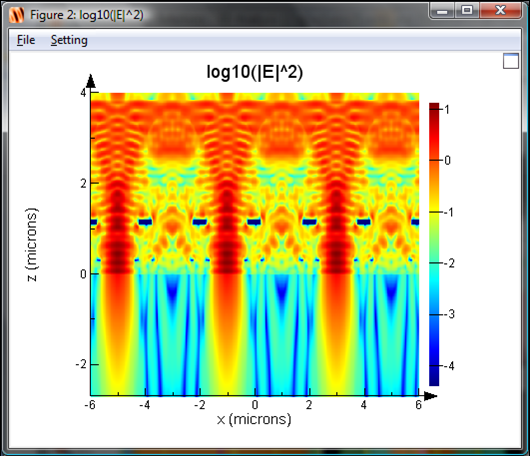
我们想用模拟计算什么？

我们想计算一些事情：

· 量子效率（QE）：这是收集的电子与入射光子的比率。QE受照明条件、物镜、图像传感器光学堆栈的光学效率（OE）和收集电子设备的效率的影响。QE的完整计算涉及光学和电气建模。

· 光学效率（OE）：这是硅中产生的电子与入射光子数量的比率，是QE计算的关键组成部分。与QE一样，这取决于照明条件、物镜和图像传感器的光学堆栈。通常，我们在OE中包含QE的某些方面，例如，仅计算在特定体积的硅中产生的光子，其中它们很有可能被收集电子设备收集。但是，我们仍然将其称为OE，并将术语QE保留用于涉及光学和电气建模的计算。

· 光学串扰、点扩散函数（PSF）和调制传递函数（MTF）：相机解析空间特征的能力可以通过PSF及其傅里叶变换MTF来测量。这些数量取决于物镜、光学堆栈和收集电子设备。在数码相机中，这些量的定义更为复杂，因为图像传感器的像素会给问题带来数字化的离散性。

· 光谱串扰和颜色矩阵系数：我们可以确定不同像素的响应，例如红光、绿光和蓝光对任何波长的响应，从而确定光谱串扰。此信息可用于确定可用于校正图像颜色的颜色矩阵系数，但是，颜色矩阵中的大、负、非对角线项会导致信噪比 （S/N） 降低，理想情况下希望避免。

· 电串扰：当一个像素下产生的电子被相邻像素捕获时，就会发生电串扰。这种类型的串扰将有助于点扩散函数和频谱串扰。对这种效应进行建模需要结合光学和电气建模。

照明条件

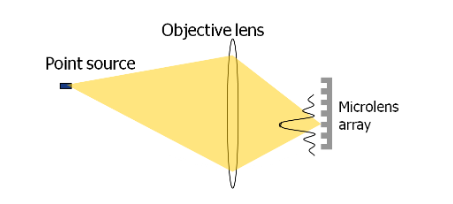
我们想要计算的几乎任何东西都取决于照明条件和物镜。下图显示了距离相机较远的点光源对系统的照明。该点光源将向下聚焦到图像传感器表面的艾里圆盘状光斑。这种类型的照明可用于计算PSF，但是，必须小心，因为我们需要考虑图像传感器上的数字化像素可能发生的各种光斑对齐。

对于许多仿真结果（QE、OE、光谱串扰、颜色矩阵系数、电串扰），我们通常对均匀照明的情况感兴趣。这是物体填满相机整个视野的情况。下图描述了这种情况。大物体由大量点光源组成，每个点光源都发出不连贯的光。这将在图像传感器表面产生不相干的艾里圆盘状斑点的总和。所有结果，所有感兴趣的电场强度量（|E|2）在硅片中，OE可以简单地通过不连贯地对每个单独仿真的结果求和或平均来计算。

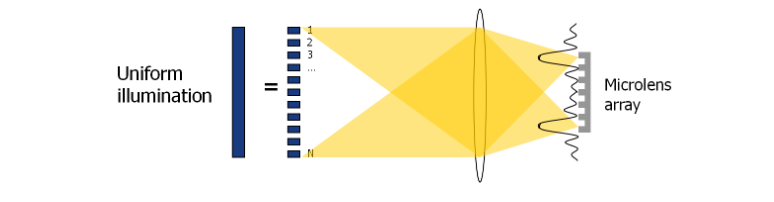
在均匀照明下，硅中的电场强度由每次模拟强度的不相干总和给出。OE 由每个模拟的平均 OE 给出。

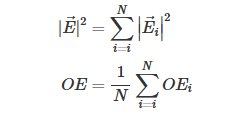
实际上，这意味着对每个光束位置运行新的仿真，并以不连贯的方式对所有结果求和或平均。由于图像传感器阵列是局部周期性的，我们只需要在一个单元（通常涉及 2×2 子像素）上执行此操作。事实上，一旦我们获得了单个单元的结果，我们就可以使用这些结果不仅计算对均匀照明的响应，还计算对其他类型的照明的响应，例如理想情况下应该照亮一个完整像素的物体的照明。这是用于计算点扩散函数中的 PSF 的方法。

实现均匀照明的最有效方法

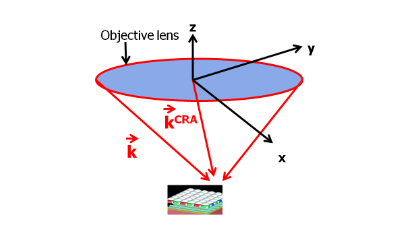
可以证明，上述均匀照明条件在数学上等价于物镜支持的所有平面波的加权非相干和（详见Jérôme Vaillant等人）。下图以图形方式描绘了这一点，我们可以看到物镜支持的不同可能入射角。

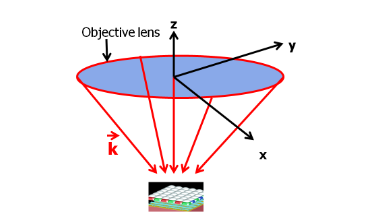
系统在均匀照明下的响应等于物镜支持的所有入射角平面波的不相干加权积分。

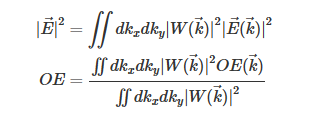
重量因子W是物镜和像素位置的属性。在低数值孔径系统中，中心像素的W的良好近似值是

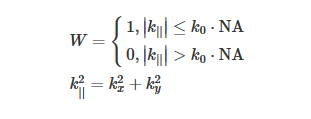
其中 k||是面内波矢量，NA是物镜的数值孔径。换句话说，对于物镜支持的所有角度，W为1，对于所有其他角度，W为0。

下图显示了图像传感器边缘附近像素的情况。在这种情况下，入射角的范围变得不对称。我们将主射线角（CRA）定义为从物镜中心到所考虑像素的光线。

用于计算均匀照明下的场强和OE的权重因子随像素的位置而变化。低数值孔径系统中边缘像素的W的良好近似值为

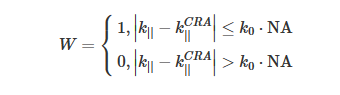
其中 k||是面内波矢量，k||CRA是CRA的面内波矢量，NA是物镜的数值孔径。换句话说，W只是通过面内CRA波矢量在k空间中移动。

因此，QE和OE的计算与角响应曲线的积分计算相同。请注意，虽然

· 这个积分实际上是在面内 k 而不是角度上，尽管低 NA 系统几乎没有区别，因为 k||/k0 = sin（q） ~q 当 q << 1 时。

· 这实际上是 kx 和 ky 上的二维积分

典型的角响应曲线如下所示，作为kx/k0的函数。在第一个图中，我们看到积分窗口以kx=0为中心，这对应于在均匀照明下计算中心像素的OE。第二条曲线显示了边缘像素的积分窗口，该像素覆盖相同的2NA大小，但被CRA的kx偏移。

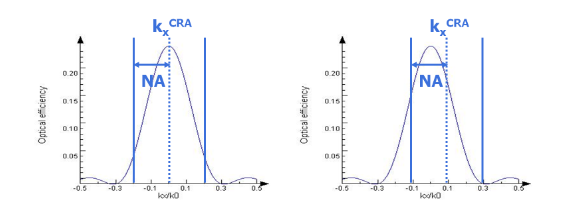
现在我们了解了均匀照明下角响应曲线与OE、QE或电场强度之间的重要关系，我们可以看到可以采取一些简单的步骤来优化图像传感器的OE：

· 我们只能模拟与CRA对应的一个平面波，即积分窗口中心的角度。如果我们尝试在这个角度优化OE，我们可能会改进整个积分。这通常是通过移动微透镜和其他层来实现的，其效果是将角响应曲线的峰值移动到积分窗口的中心，从而最大化积分。这是一种非常有效的方法，可以在均匀照明下优化系统的OE，而无需进行大量仿真。在计算微透镜位移时各种CRA的最佳微透镜位移时，采用这种方法。在这种方法中，我们实际上是通过仅对积分窗口中心的一个点进行采样来估计积分。

· 我们可以模拟对应于CRA的平面波和积分窗口边缘附近的几个角度，并将这些结果与一定的权重相结合。在这种方法中，我们试图通过最大化积分窗口中心和积分窗口边缘的函数来优化积分 – 基本上我们仅通过采样几个点来估计积分。由于角响应曲线在积分窗口上通常是一个相当平滑的函数，因此这种方法应该最大化我们的真正积分。在优化微透镜 ROC 中优化透镜曲率半径时，将采用此方法。

· 我们可以运行足够的模拟来正确计算角度响应曲线并正确计算积分。这显然是最准确的方法，但可能涉及大量模拟，特别是对于我们需要对kx和ky进行采样的3D模拟。每个点仅采样 10 个点会导致 10×10=100 个不同的入射角。尽管如此，这种方法可以与均匀照明下的OE实验结果非常吻合。

获得非极化结果

非偏振结果可以通过不相干地平均 2 个正交极化（通常为 S 和 P）从偏振结果中获得。有关证明和更多详细信息，请参阅非偏振光束。不幸的是，这意味着我们必须对每个光束或平面波运行 2 次仿真才能获得非极化结果。最初，可能需要仅使用一个偏振并忽略偏振效应以节省时间，但在这些长度尺度上，S和P极化的结果存在差异，最终结果不应忽略这些效应。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删