复合材料可以发挥各种材料的优点,克服单一材料的缺陷,提高强度、弹性模量及断裂韧性等,扩大材料的应用范围。由于单一材料性质的改变比较困难,但将不同性质的材料相互复合能够形成种类丰富的材料,而表现出千差万别的材料性能,所以复合材料在新材料技术的研发过程中占有重要作用,其设计的自由性是其他材料所无法比拟的。复合材料由于其优良的综合性能,特别是其性能的可设计性被广泛应用于航空航天、国防、交通、体育等领域。
1 改性复合材料的本构理论与建模方法
颗粒或短纤维增强复合材料属于复合材料家族,与连续纤维增强树脂基复合材料相比,其材料可设计性更为灵活多样,这种针对材料性能设计的科研活动,根据材料体系的是否发生根本变化和是否有全新材料性能的出现,通常可分为新材料研发或原材料改性。材料的改性是材料研究领域的一项长期普遍的研究内容。针对力学性能研究,首先需要研究该材料的本构关系。研究方法一般是利用基于应变梯度塑性理论的本构方程表征局域区和内部结构的长度-尺度依赖性,此外,用应变梯度塑性理论进行正则化,大大降低了计算力学中广为接受的有限单元法计算结果对网格的依赖性。因此,应变梯度理论似乎提供一个直接的塑性流动的尺寸效应进行建模在连续介质力学方法。因此,应变梯度理论提供了一种在连续介质力学方法中模拟塑性流动尺寸效应的直接方法。
为了表示本构方程,可采用更新的拉格朗日公式,其中每个物质粒子用坐标标记。对于弹塑性固体,假设变形速率梯度的对称部分分解为弹性部分和塑性部分。进而有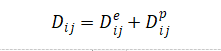 (1.1)
(1.1)
弹性响应假定是各向同性的,并由胡克定律表示: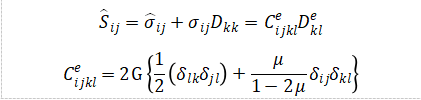 (1.2)
(1.2)
其中G为弹性剪切模量,为泊松比,, 分别为基尔霍夫应力和柯西应力在当前状态下的Jaumann速率。
利用Mises型流动规律,得到了与应变梯度相关的塑性应变率的本构方程为:
(1.3)
式中为柯西应力偏量部分,为等效应力,为等效塑性应变率。
与应变速率无关的材料的屈服函数变为: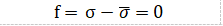
(1.4)
与应变梯度相关的流动应力可以沿着相同的线表示,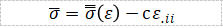
(1.5)
其中,是常规的加工硬化函数,第二项表示应变梯度相关项。是描述对应变梯度依赖程度的系数。通过式(4)和式(5),一致性条件f=0变为: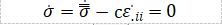
(1.6)
结合式(1.1)-式(1.3)推导了弹塑性本构方程: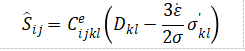
(1.7)
由式(1.6)计算出等效应变率,可将等效应变率视为自变量;将在下一节中说明的变分原理变得非常简单,并且可以建立采用常规单元的有限元方程。
推导与应变梯度相关的应变速率相关材料的本构方程是简单的。相应的表达式为式(1.5),其中流动应力由应变率相关的应力代替。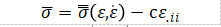
(1.8)
弹粘塑性材料的本构方程为式(1.7),将式(1.8)中的流动应力替换为与温度有关的流动应力,得到与温度有关的材料的相应表达式(1.7)。
在低阶应变梯度塑性理论中,由于其本构关系中不包含应力的高阶项,平衡方程和边界条件都和经典塑性理论保持一样,只是通过位错理论中引入了表征材料尺度效应的特特征长度,之后进一步修改应变率来改进低阶应变梯度塑性理论,使得其和经典塑性理论得到很好的对应。所以在有限元实现中特别容易,不需要重新定义单元类型,这就大大的减小了有限元实现的工作量。
为了模拟细观力学问题,主要是通过编写有限元软件 ABAQUS中的用户自定义子程序(UMAT),考虑将低阶应变梯度塑性理论中的材料本构关系编写在微观力学分析当中,进而实现低阶应变梯度塑性理论的有限元分析。细观力学计算的目的主要是通过数值模拟的方法得到材料宏观材料参数。在对实际工程结构进行强度和刚度校核或优化设计时,需要输入这些宏观材料本构参数。
2 基于ABAQUS的细观力学计算
以Al基SiC复合材料为例,SiC颗粒相对于Al基体十分坚硬,所以将SiC颗粒假设为各项同性的线弹性材料,随着颗粒的直径从16微米减小到75微米,看其受单轴均匀拉伸时的受力。需要在子程序中输入的参数如表2.1所示。 表2.1 输入参数
表2.1 输入参数
G Env Stress() Power ExpM alpha BV Sigma() Cp Toler
基体 28600 0.33 208 0.136 20 0.3 0.283 0 1 1e-8
颗粒 182480 0.17
G剪切模量、Env泊松比、Stress()为初始屈服应力、Power为塑性硬化指数、ExpM为率敏感系数、alpha经验值系数、BV为Burgers矢量、Sigma()为摩擦应力、Cp为硬化关系中的参数、Toler为激活塑性应变增量的指标。其中应力单位均为MPa。
在掌握了低阶应变梯度塑性理论的本构关系之后,完成UMAT子程序的编写,编出四节点四边形单元,掌握了颗粒增强复合材料的细观分布之后,建立以代表性体积单元为窗口施加周期性边界条件的有限元模型,如图2.1所示。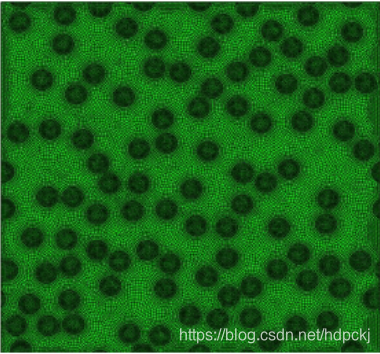
图2.1 四节点四边形单元的微观结构模型
图2.1是一个有着100个均匀分布颗粒,颗粒体积分数有10%的等效体积单元网格的细观模型。模型尺寸20 x 20,单位是微米。沿着Y轴方向施加均匀的拉应力。模型中颗粒和基体之间不考虑界面因素的影响。为了使模型更符合实验现象,采用周期性边界条件,采用的周期性边界条件可以满足变形后的协调性和对称性,保证了边界上的切应力为零,并且使得边界上的法向位移一致,这样模型的变形就保证了内部的变形连续性。由于此算例是单轴拉伸载荷,所以模型的两个侧面上的合力为零。
为了直观地分析模型的变形和应力分布,需要从模型的应力云图去观察。在把模型提交到ABAQUS之后,提取结果文件观察基体颗粒应力云图及等效塑性应变梯度云图,如图2.2所示。
图2.2 单轴拉伸下模型的应力云图:(a)Mises应力云图,(b)等效塑性应变梯度云图
图2.2(a)中显示的是在沿着Y轴方向施加位移载荷之后的应力云图,可以看出,应力分布比较均匀,最大应力发生在颗粒和基体的界面上,而且由于施加的载荷是沿着y方向的均匀拉伸,所以整个模型中比较大的应力分布是沿着y方向均匀分布的,图形中出现很少的应力集中现象,整的来说影响并不大。图2(b)表示的是基体发生塑性变形后的等效塑性应变梯度云图,可见虽然在离颗粒较远的基体上有些塑性应变比较大,不过总的来说基体的塑性应变还是均匀的。从图中可知,由于周期性边界条件的施加,在施加了轴向位移载荷之后模型的变形不像是自由边界条件那样光滑,而是在四周出现不光滑的变形。
3 增韧复合材料仿真与力学性能计算
为了保证仿真模型的真实性,复合材料中的颗粒可由MATLAB随机产生, MATLAB生成的多边形颗粒的有限元模型及基体、颗粒和界面的放大图如图3.1所示。
图3.1 多边形颗粒的有限元结构模型
SiC颗粒相对于铝基体十分坚硬,所以我们把SiC颗粒假设为各项同性的线弹性材料,由此假设得出颗粒的弹性模量和泊松比: E= 420GPa,u=0.17。颗粒的强度服从韦伯尔分布,平均强度为 = 550MPa,形状参数为m = 9.62。描述颗粒的损伤初始用的是最大主应力准则,通过ABAQUS中的子程序USDFLD实现。
采用颗粒的半径为R=20微米,颗粒的个数为100,颗粒的体积分数为25 %。在保持颗粒强度为550MPa不变的情况下,改变界面强度分别为275MPa, 550MPa和1100MPa,进而得出界面强度对金属基复合材料的强度和损伤演化的影响。
3.1 拉/压性能的仿真及计算结果分析
在本节中,对不同体积分数下模型的界面强度和颗粒排列在单轴拉伸载荷作用下复合材料的应力应变关系进行了研究。为了消除模型中的误差,本节模拟分析了15个模型,通过分析这15个模型的损伤起始应力及相应应变起始损伤应变和颗粒完全损伤时的应力及相应应变的均值和标准偏差,保留较为理想的5组模型,这五组模型的应力应变曲线及相应的特征点绘制如图3.2所示。
图3.2单轴拉伸下不同微观结构模型的名义应力应变关系曲线:(a)界面强度为275MPa,(b)界面强度为550MPa,(c)界面强度为1100MPa
单轴拉伸下不同微观结构模型的名义应力应变关系曲线,其中(a) , (b) , (c)分别代表界面强度为275MPa, 550MPa和1100MPa情况下的应力应变曲线。可以看出,细观力学模型中的颗粒排列在应力应变关系中的作用不大,并且图5.4中都表现出相同的趋势,即随着界面强度不断增强,颗粒损伤起始和结束时的应力不断增强。
为了更好的观察模型的变形和应力分布,三种界面强度模型在拉伸作用下的应力云图如图3.3所示。
图3.3单轴拉伸作用下不同界面强度模型的应力云图:(a)界面强度为275MPa,
(b)界面强度为SSOMPa,(c)界面强度为1100MPa
3.2 剪切性能的仿真及计算结果分析
在本节中,研究了纯剪切载荷作用下模型的界面强度和颗粒排列对复合材料的宏观应力应变关系。五组模型的应力应变曲线绘制如图3.4所示。
图3.4表示了颗粒体积分数为25%时,界面强度和颗粒排列对金属基复合材料强度与损伤演化过程的影响,其中(a)表示颗粒和界面间的界面强度为275MPa时,纯剪切作用下的名义应力应变曲线,(b)表示颗粒和界面间的界面强度为550MPa时,纯剪切作用下的名义应力应变曲线,(c)表示颗粒和界面间的界面强度为1100MPa时,纯剪切作用下的名义应力应变曲线。图中可以看出,细观力学模型中的颗粒排列对材料线性部分和损伤后的基体承载部分的应力应变曲线影响不大。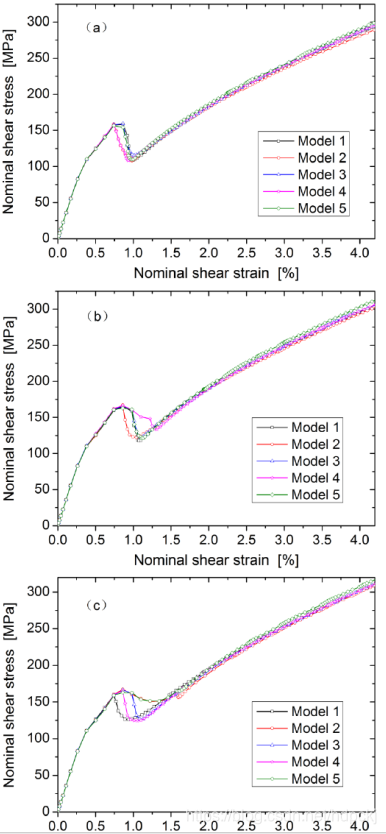
图3.4纯剪作用下不同微观结构模型的名义应力应变关系曲线:(a)界面强度为275MPa,(b)界面强度为550MPa,©界面强度为1100MPa
为了更好地观察模型的变形和应力分布,图3.5列举了在颗粒分数为25%时,三种界面强度模型在单剪作用下的应力云图。
图3.5纯剪作用下不同界面强度下模型的应力云图: (a)界面强度为275MPa,(b)界面强度为550MPa,©界面强度为1100MPa
3.3 增韧复合材料结构的宏观失效模拟
在本节中,界面强度和颗粒排列对复合宏观应力一应变拉剪藕合载荷下的关系进行了研究。剪切应变为拉伸应变的1.0倍,记作k=1.0,对载荷下的微观结构模型进行有限元分析。五组模型的应力应变曲线绘制如图3.6所示。
从图中可以看出在拉剪藕合作用下,界面强度对材料损伤破坏阶段的拉伸应力应变曲线影响很大,但是对剪切应力应变曲线几乎没有影响。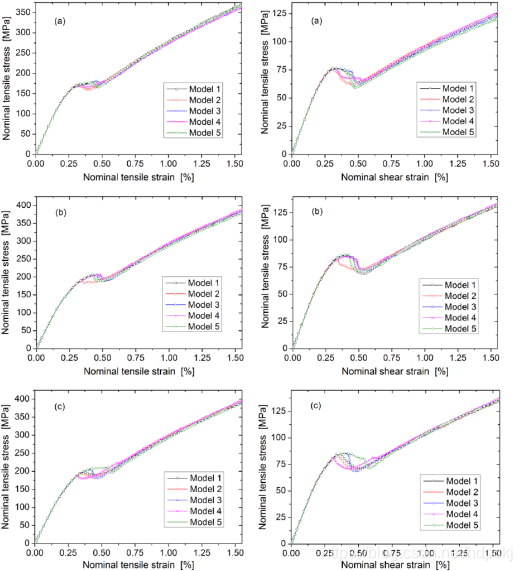
图3.6 k=1.0时拉剪藕合作用下不同微观结构模型的名义拉伸应力应变关系曲线(左),名义剪切应力应变关系曲线(右)
为了更好的观察模型的变形和应力分布,图5.3.7列举了在颗粒分数为25%且藕合方式为加载藕合和拉伸比例为1.0时,三种界面强度下模型的应力云图。
图3.7三种界面强度下模型的应力云图:(a)界面强度为275MPa,(b)
界面强度为550MPa,(c)界面强度为1100MPa
实例分析:颗粒增强金属基复合材料结构建模、拉伸过程及失效分析
颗粒增强金属基复合材料中,颗粒相一般为各向同性弹性材料,如SiC材料,弹性模量为400GPa,泊松比为0.2,基体相为金属材料,一般为各向同性弹塑性材料,等向强化模型,如纯铝材料,弹性模量为70GPa,泊松比为0.33,见表3.7.1所示。
表3.7.1 材料参数

图3.7.1 多颗粒随机分布几何模型
图3.7.2 划分网格
图3.7.3增强颗粒等效应力云图
图3.7.4 增强颗粒应变云图
图3.7.5 基体等效应力云图
图3.7.6 基体等效塑性应变云图
由于颗粒相与基体相弹性模量的不匹配,在颗粒相与基体相接触的界面会产生显
著的应力集中。图3.7.3和3.7.4分别是X方向单轴应变加载到0.04时的颗粒等效应力
云图和颗粒等效应变云图。图3.7.5和图3.7.6是基体等效应力云图和基体等效塑性应变
云图。
从图3.7.3和图3.7.4可以看出,颗粒相的应力集中很明显,而且相当大,由图3.7.5和图3.7.6可知,基体中的等效应力和等效塑性应变还是处于较正常的范围。而且在界面处当达到一定应力后,界面将产生裂纹甚至开裂。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删