信号去噪新方法：VNCMD实现多信号模式下非线性噪声去噪

🔥 内容介绍

信号去噪是一项重要的信号处理技术，它在多个领域中发挥着关键作用。无论是在通信系统中，医学成像中，还是在音频处理中，信号去噪都能有效地提高信号质量和准确性。近年来，基于变分非线性线性调频模式分解（Variational Nonlinear Chirp Mode Decomposition，VNCMD）的方法在多信号模式下非线性噪声去噪方面取得了显著的成果。本文将介绍VNCMD方法以及它在信号去噪中的应用。

VNCMD是一种基于变分方法的信号分解技术，它能够将信号分解为多个模式。与传统的线性调频模式分解方法不同，VNCMD能够处理非线性调频信号，并且对噪声具有较好的鲁棒性。这使得VNCMD在处理包含非线性噪声的多信号模式时具有优势。

VNCMD的基本原理是通过最小化信号与模式之间的差异来实现信号的分解。具体而言，VNCMD通过最小化信号与模式之间的差异的二阶范数来获得分解后的模式。这种基于变分方法的分解能够有效地提取信号中的主要模式，并且对噪声的影响较小。

在多信号模式下的非线性噪声去噪中，VNCMD方法能够将信号分解为多个模式，其中包括信号的主要模式和噪声的模式。通过对噪声模式的分析和处理，VNCMD能够准确地去除信号中的非线性噪声。这使得VNCMD在处理复杂信号中的噪声问题时具有较好的效果。

VNCMD方法在信号去噪中的应用已经得到了广泛的研究和实践。例如，在语音信号去噪中，VNCMD能够有效地去除环境噪声，提高语音信号的清晰度和可懂性。在医学成像中，VNCMD能够准确地提取出病灶信号，并去除噪声干扰，从而提高诊断的准确性。在音频处理中，VNCMD能够去除音频信号中的杂音和失真，提高音频的质量。

然而，尽管VNCMD方法在信号去噪中具有较好的效果，但它仍然存在一些挑战和限制。首先，VNCMD方法的计算复杂度较高，需要大量的计算资源。其次，VNCMD方法对信号的模式数量和噪声的特性较为敏感，需要进行合理的参数选择和调整。此外，VNCMD方法在处理非平稳信号时可能存在一定的局限性。

综上所述，基于变分非线性线性调频模式分解的VNCMD方法在多信号模式下非线性噪声去噪方面具有较好的效果。它能够有效地提取信号中的主要模式，并去除非线性噪声的影响。然而，VNCMD方法仍然需要进一步的研究和改进，以提高其计算效率和适用性。相信随着技术的不断发展，VNCMD方法将在信号处理领域发挥越来越重要的作用。

📣 部分代码

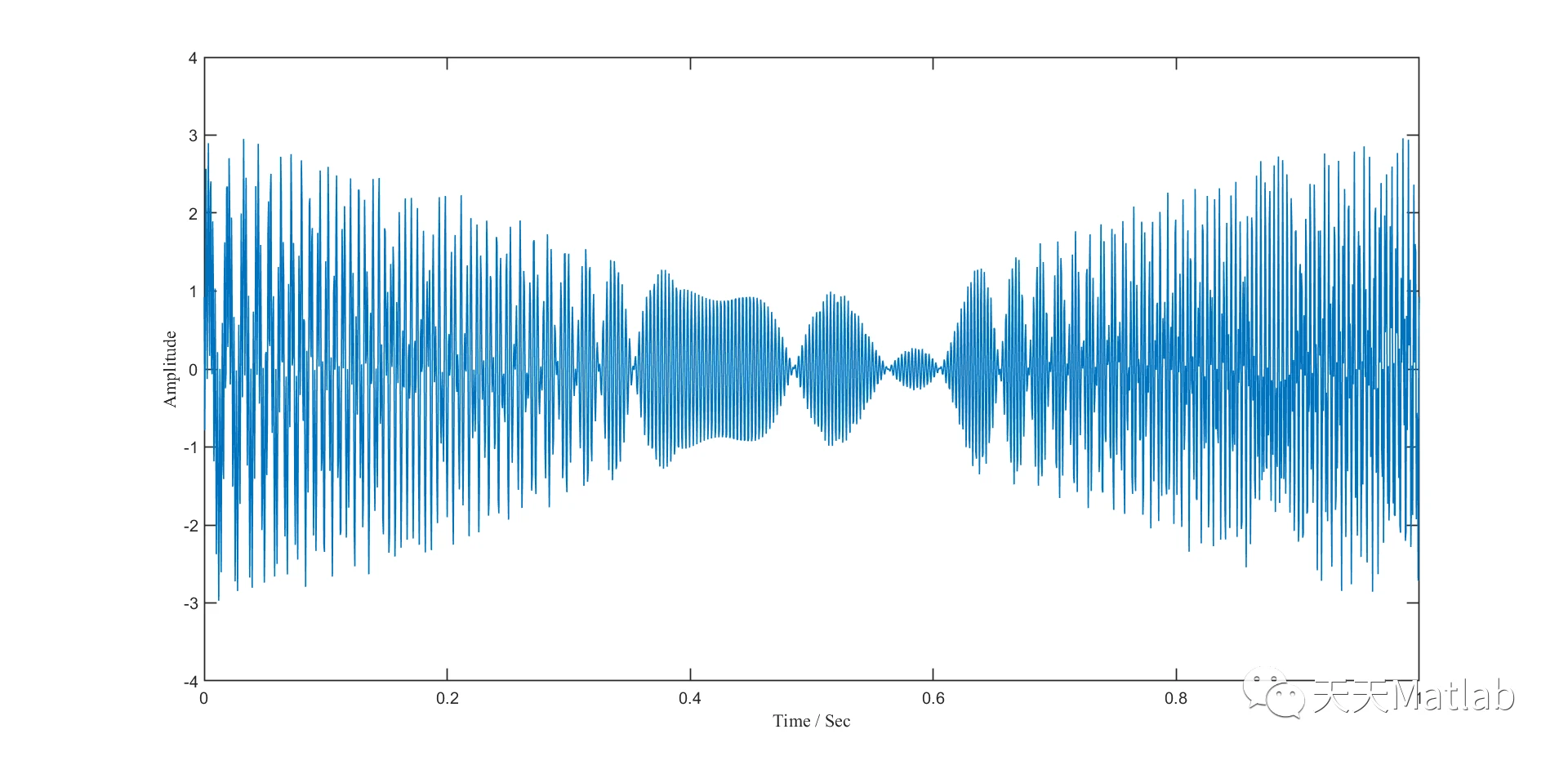
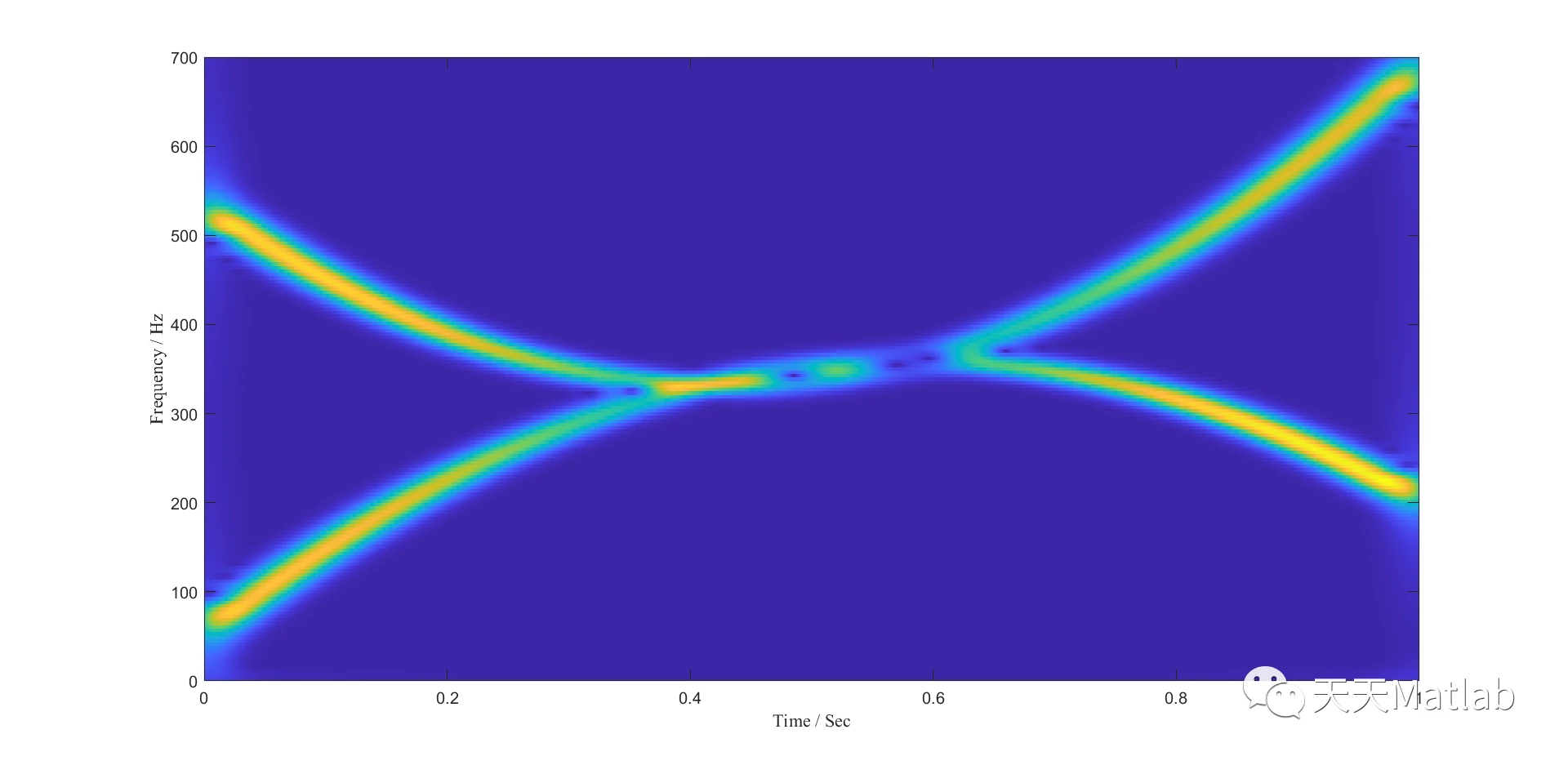
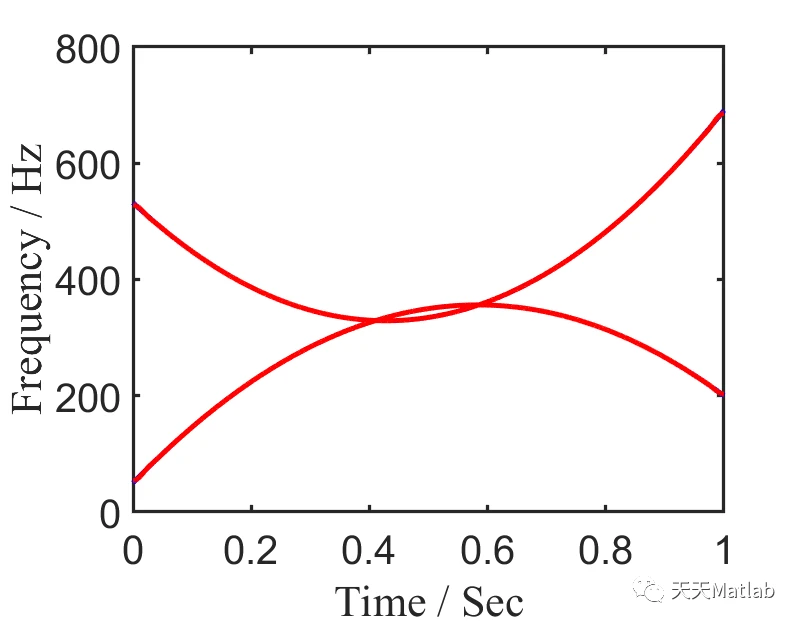
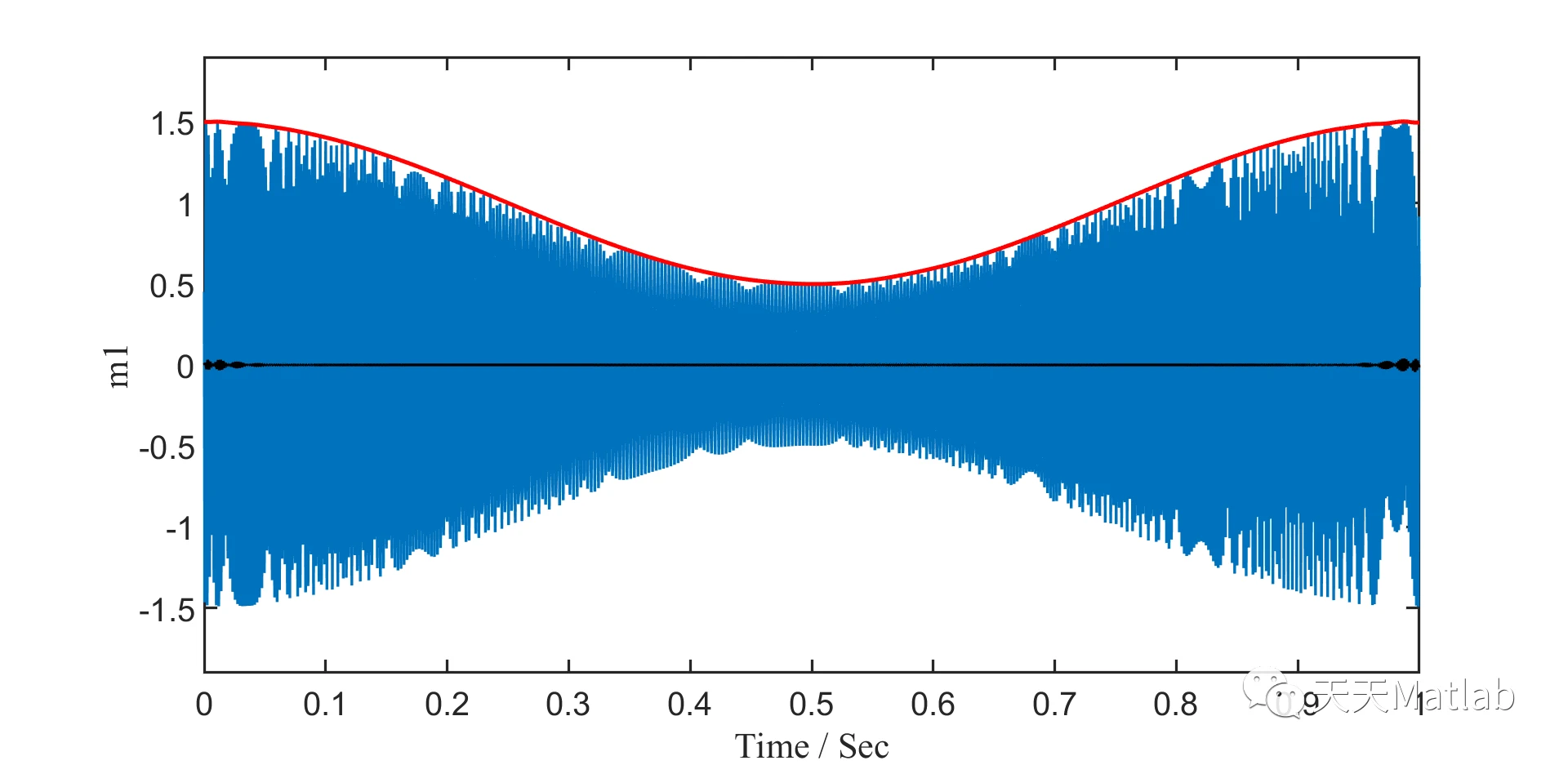
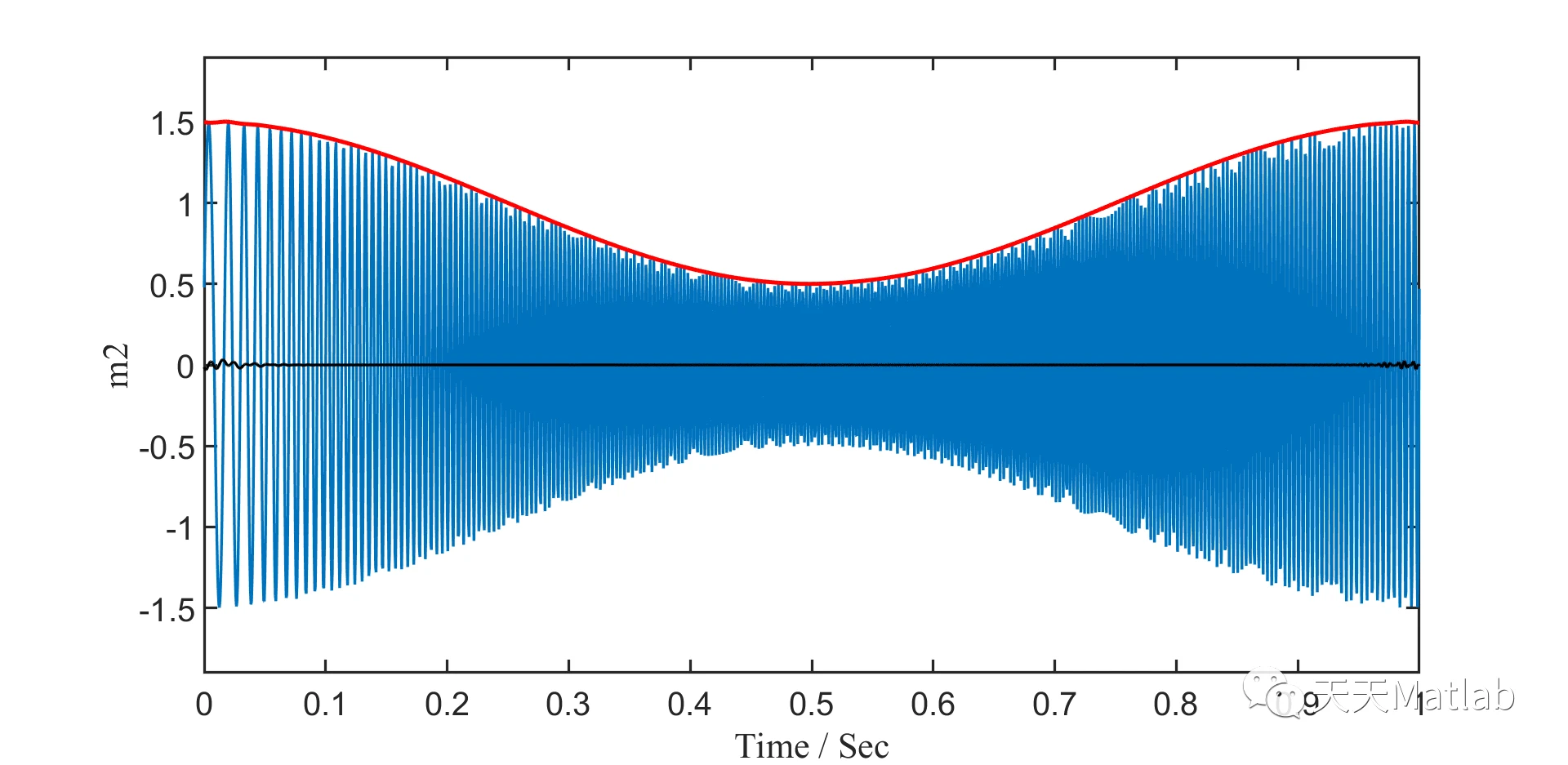
%%%%%%%%%%%%%% signal with intersecting IFs %%%%%%%%%%%%%%%%%clcclearclose allSampFreq = 2000;t = 0:1/SampFreq:1;Sig1 = (1+0.5*cos(2*pi*t)).*cos(2*pi*(0.2 + 532*t -474*t.^2 + 369*t.^3));IF1 = 532 - 948*t + 1107*t.^2;Sig2 = (1+0.5*cos(2*pi*t)).*cos(2*pi*(0.8+50*t + 525*t.^2 -300*t.^3));IF2 = 50 + 1050*t - 900*t.^2;Sig = Sig1+Sig2;figureset(gcf,'Position',[20 100 320 250]); set(gcf,'Color','w'); plot(t,Sig,'linewidth',1);xlabel('Time / Sec','FontSize',12,'FontName','Times New Roman');ylabel('Amplitude','FontSize',12,'FontName','Times New Roman');set(gca,'xtick',[0 0.2 0.4 0.6 0.8 1]);set(gca,'FontSize',12)set(gca,'linewidth',1);axis([0 1 -4 4])%% STFTRatio = 0;figure[Spec,f] = STFT(Sig',SampFreq,512,256);imagesc(t,f,abs(Spec)); axis([0 1 0 700]);set(gcf,'Position',[20 100 320 250]); xlabel('Time / Sec','FontSize',12,'FontName','Times New Roman');ylabel('Frequency / Hz','FontSize',12,'FontName','Times New Roman');set(gca,'xtick',[0 0.2 0.4 0.6 0.8 1]);set(gca,'YDir','normal')set(gca,'FontSize',12);set(gcf,'Color','w'); %% parameter settinginiIF = [700*ones(1,length(t));20*ones(1,length(t))];% initial guess for the IFs for the three signal modesalpha = 5e-6; beta = 1e-6; % this parameter can be smaller which will be helpful for the convergence, but it may cannot properly track fast varying IFsvar = 0;% noise variancetol = 1e-8;%tic[IFmset IA smset] = VNCMD(Sig,SampFreq,iniIF,alpha,beta,var,tol);toc%% Relative errors of the finally estimated IFs RE1 = norm(IFmset(1,:,end)-IF1)/norm(IF1) RE2 = norm(IFmset(2,:,end)-IF2)/norm(IF2)%% estimated IFfigureplot(t,[IF1;IF2],'b','linewidth',3) % true IFshold onplot(t,IFmset(:,:,end),'r','linewidth',3) % finally estimated IFsset(gcf,'Position',[20 100 640 500]); xlabel('Time / Sec','FontSize',24,'FontName','Times New Roman');ylabel('Frequency / Hz','FontSize',24,'FontName','Times New Roman');set(gca,'xtick',[0 0.2 0.4 0.6 0.8 1]);set(gca,'YDir','normal')set(gca,'FontSize',24);set(gca,'linewidth',2);set(gcf,'Color','w'); axis([0 1 0 800])%% Reconstructed modesfigureset(gcf,'Position',[20 100 640 200]); set(gcf,'Color','w'); plot(t,smset(1,:,end),'linewidth',2) % estimated modehold onplot(t,Sig1 - smset(1,:,end),'k','linewidth',2) % estimation errorshold onplot(t,IA(1,:),'r','linewidth',3) % estimated IAsxlabel('Time / Sec','FontSize',24,'FontName','Times New Roman');ylabel('m1','FontSize',24,'FontName','Times New Roman');set(gca,'YDir','normal')set(gca,'FontSize',24);set(gca,'linewidth',2); axis([0 1 -1.9 1.9])figureset(gcf,'Position',[20 100 640 200]); set(gcf,'Color','w'); plot(t,smset(2,:,end),'linewidth',2) % estimated modehold onplot(t,Sig2 - smset(2,:,end),'k','linewidth',2) % estimation errorshold onplot(t,IA(2,:),'r','linewidth',3) % estimated IAsxlabel('Time / Sec','FontSize',24,'FontName','Times New Roman');ylabel('m2','FontSize',24,'FontName','Times New Roman');set(gca,'YDir','normal')set(gca,'FontSize',24);set(gca,'linewidth',2); axis([0 1 -1.9 1.9])