内容介绍

多径衰落信道是无线通信领域中不可避免的现象，特别是在城市和室内环境中。这种现象会导致无线信号在传输过程中出现多个路径，从而影响信号的传输质量。因此，对于无线通信系统的设计和优化，了解多径衰落信道的特性是非常重要的。

为了更好地理解和研究多径衰落信道，我们可以使用信道仿真技术。信道仿真可以帮助我们模拟多种不同的信道环境，并通过模拟结果来评估不同的通信系统的性能。在这篇文章中，我们将介绍如何基于实现无线通信多径衰落信道仿真。

首先，我们需要了解多径衰落信道的基本特性。多径衰落信道是指无线信号在传输过程中经历多个路径，这些路径的长度和方向可能不同，从而导致信号的干扰和衰落。这种干扰和衰落的程度取决于信号的频率、传输距离、环境和天线高度等因素。

接下来，我们需要选择一个信道仿真工具来实现多径衰落信道仿真。有很多不同的信道仿真工具可供选择，例如MATLAB、NS-3、Opnet等。在这篇文章中，我们将使用MATLAB作为信道仿真工具。

在MATLAB中，我们可以使用MATLAB Communications Toolbox来实现无线通信多径衰落信道仿真。该工具箱提供了多个函数和工具，可以帮助我们生成不同类型的信道模型，并模拟信号在这些信道模型中的传输。下面是一个简单的MATLAB代码示例，用于生成一个瑞利衰落信道：

% Set up the channel parameters fc = 2.4e9; % carrier frequency fs = 10e6; % sampling frequency Ts = 1/fs; % sampling time fd = 200; % maximum Doppler shift tau = [0 1e-6 3e-6]; % delay profile pdb = [0 -3 -6]; % power delay profile chan = ricianchan(Ts,fd,tau,pdb); % create the channel object

% Generate a random signal tx = randn(1000,1); % generate a random signal rx = filter(chan,tx); % pass the signal through the channel

在上面的代码中，我们首先设置了信道参数，包括载波频率、采样频率、多普勒频移、延迟和功率延迟。然后，我们使用ricianchan函数创建了一个瑞利衰落信道对象。最后，我们生成了一个随机信号，并通过filter函数将其传输到信道中。

通过这种方式，我们可以使用MATLAB Communications Toolbox来实现各种不同类型的信道模型，例如瑞利衰落信道、高斯衰落信道、Nakagami-m衰落信道等。我们还可以使用不同的参数来调整信道模型的特性，例如多普勒频移、延迟、功率延迟和信号频率等。

总之，多径衰落信道是无线通信领域中不可避免的现象，对于无线通信系统的设计和优化非常重要。通过信道仿真技术，我们可以更好地了解多径衰落信道的特性，并评估不同的通信系统的性能。MATLAB Communications Toolbox是一个非常强大的信道仿真工具，可以帮助我们实现无线通信多径衰落信道仿真。

部分代码

%多径衰落信道%按F5开始运行%主要用于多径无线接口%多径衰落信道公式和图形%M文件运行后，输入显示为蓝色%输出为红色， 输出载波变动、增加、减弱%       L%a=an*exp(-j*2*pi*fc*nT)%c=a*exp(-j*2*pi*fc*time_1);                 %g=int(c*sin(B*(v-n*T))/(B*(v-n*T)),v);                 %x=g*[zeros(1,100),signal_in]                %signal_out=symsum(x,time_1,0,N);               %       k% S(t)--------T-----T-----T-----T-------------!     Delay%          !     !     !     !     !          !  %          !     !     !     !     !          !%         *g0   *g1   *g2   *g3   *g4  ---   *gN    response                    %          !     !     !     !     !          !%          !     !     !     !     !          !%          !-----!-----!-----!-----!----------!-----Sum----r(t)signal out                                                     %时间间隔endplot(time_1,signal_out,'r')                                            %红色信号输出线figure;xlabel('频率');ylabel('振幅');title('多径衰落信道信号');grid on;                                                                   %画网格线hold onf_out=-0.5:1/N_point:0.5-1/N_point;                                        %对输出频谱图横轴fo取点signal_ff=fft(signal_out);                                                 %进行FFT变换signal_fff=signal_ff/max(signal_ff);                                       %归一化处理signal_f=fftshift(abs(signal_fff));                                        %归拢处理plot (f_out,signal_f,'r')                                                  %红色频谱图axis([x_min x_max y_min y_max])                                            %设定坐标轴取值范围hold offfigure;xlabel('频率');ylabel('振幅');title('输入信号');grid on;                                                                   %画网格线hold onf_out=-0.5:1/N_point:0.5-1/N_point;                                        %对输出频谱图横轴fo取点signal0=sin(2*pi*f*time_1);signal1=fft(signal0);                                                      %进行FFT变换signal2=signal1/max(signal1);                                              %归一化处理signal3=fftshift(abs(signal2));                                            %归拢处理plot (f_out,signal3,'r')                                                   %红色频谱图axis([x_min x_max y_min y_max])                                            %设定坐标轴取值范围%plot (f_out,abs(signal_f),'r')                                            %红色频谱图hold off%signal_out=zeros(1,2000)%for n = 1:1:N                                                             %叠代    %c=a*exp(-j*2*pi*fc*time_1(n));                                        %定义复低通冲激响应     %gg=int(c*sin(B*(v-n*T))/(B*(v-n*T)),v);                               %冲激响应函数    %g=vpa(gg);                                                            %将符号常数转变为数值常数    %signal_out=signal_out+g*[zeros(1,n*100),signal_in,zeros(1,(N-n)*100)];%输出信号    %plot (time_1,(signal_out),'r')                                        %红色输出线    %pause (0.5)                                                           %时间间隔    %end %for n =1:1:N                                                              %叠代    %c=a*exp(-j*2*pi*fc*time_1(n));                                        %定义复低通冲激响应     %g=int(c*sin(B*(v-n*T))/(B*(v-n*T)),v);                                %冲激响应函数             %x=g*[zeros(1,n*100),signal_in(1:end-(n*100))];    %signal_out=symsum(x,1,N)                                              %输出信号    %plot (time_1,(signal_out),'r')                                        %红色输出线    %pause (0.5)                                                           %时间间隔%end

运行结果

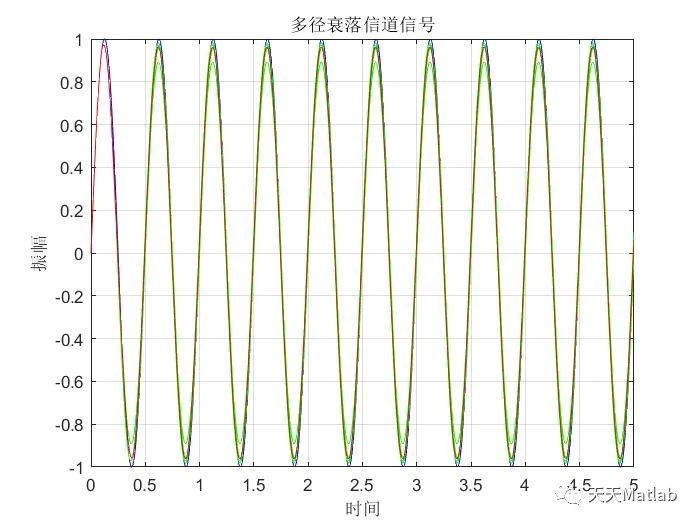
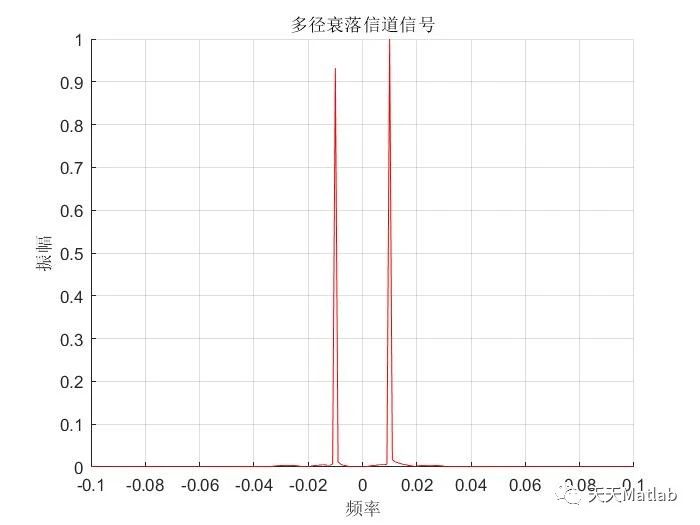
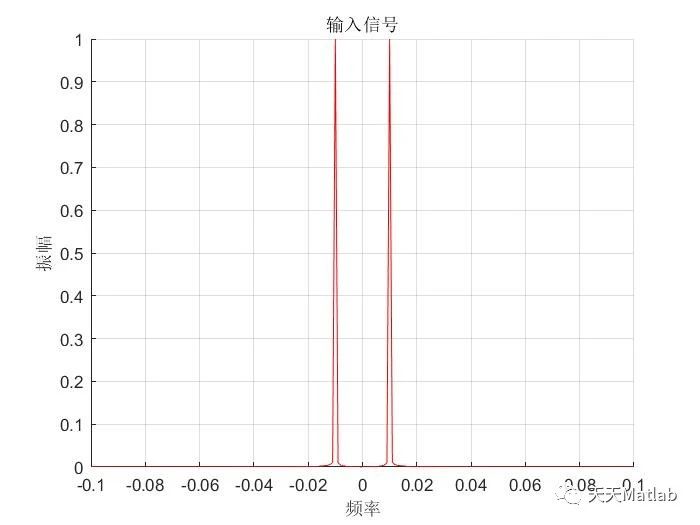
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删