MATLAB数据拟合：直观展示数据之美

数据拟合方法

　　科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据，根据这些数据，我们往往希望得到一个连续的函数（也就是曲线）或者更加密集的离散方程与已知数据相吻合，这过程就叫做拟合(fitting)。

曲线拟合也称为曲线逼近，它只要求拟合的曲线合理的反应数据的基本趋势，而并不要求曲线一定经过数据点，只是要求在整体上“尽量好”的逼近原函数。这时,在每个已知点上就会有误差,数据拟合就是从整体上使误差,尽量的小一些。

曲线拟合有几种不同的判别准则，如使偏差的绝对值之和最小、使偏差的最大绝对值最小和使偏差的平方和最小（即最小二乘法）等方法，最常用的方法就是最小二乘法。

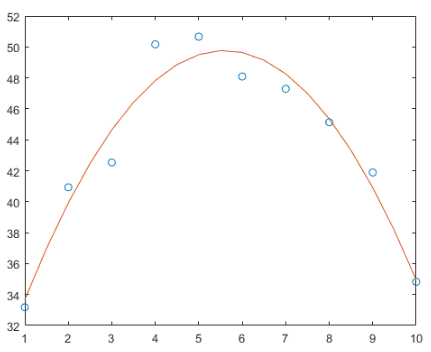
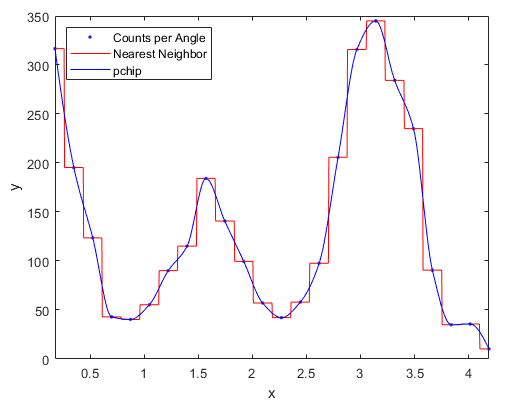
通过软件MATLAB，我们可以很方便的对已经采集到的数据点进行拟合，效果如下所示：

绘制拟合结果图

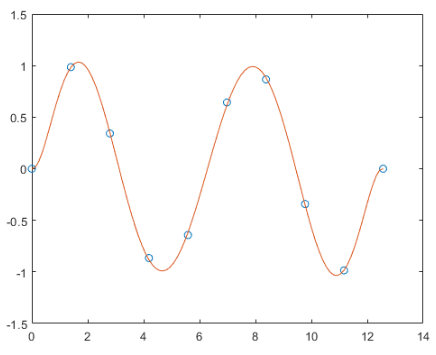
进行预测，看之后某些点的走向

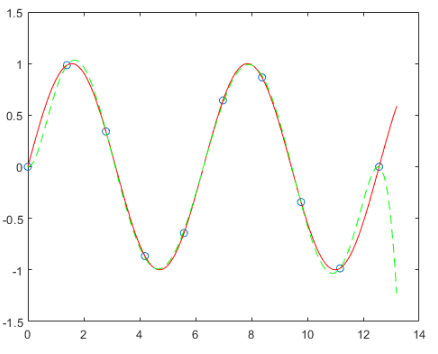
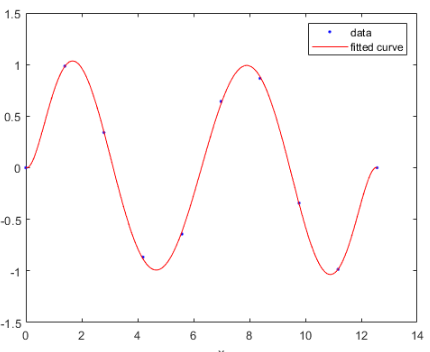
在MATLAB中还可以利用更为强大的FIT函数

一维多项式拟合（曲线）

二维多项式拟合（曲面）

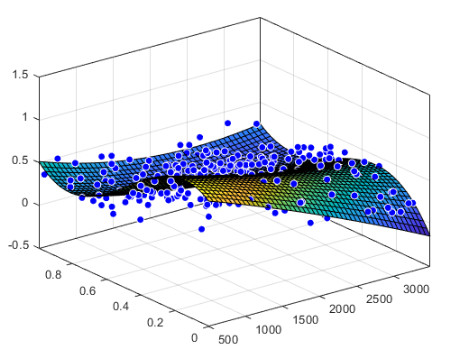
对于同一数据，指定不同的拟合参数和类型

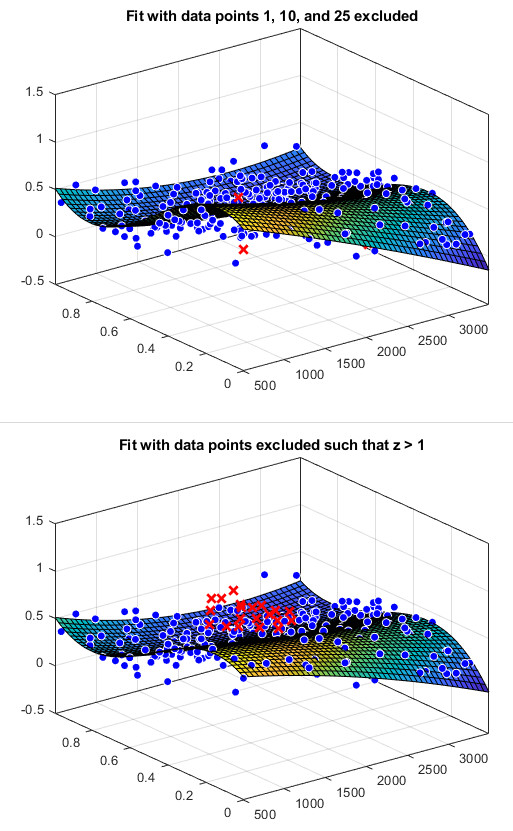
曲面情况下剔除部分点，并在图中标记

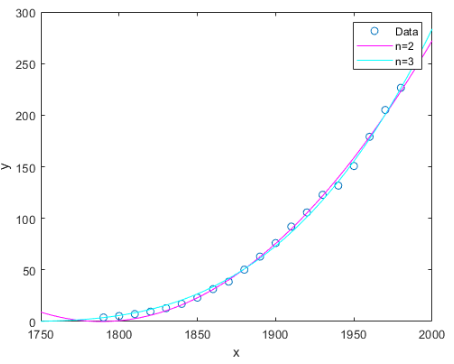
对于同一数据，指定滑动平均公式的不同参数和类型

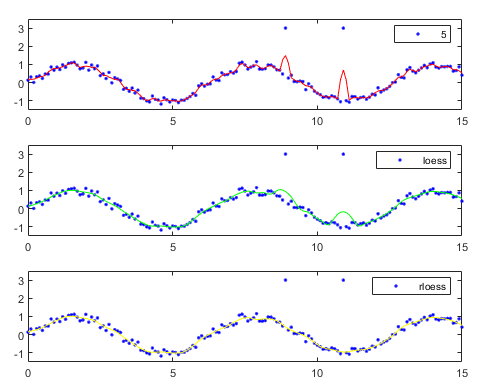
使用fit函数进行平滑（消除个别异常数据点带来的影响）

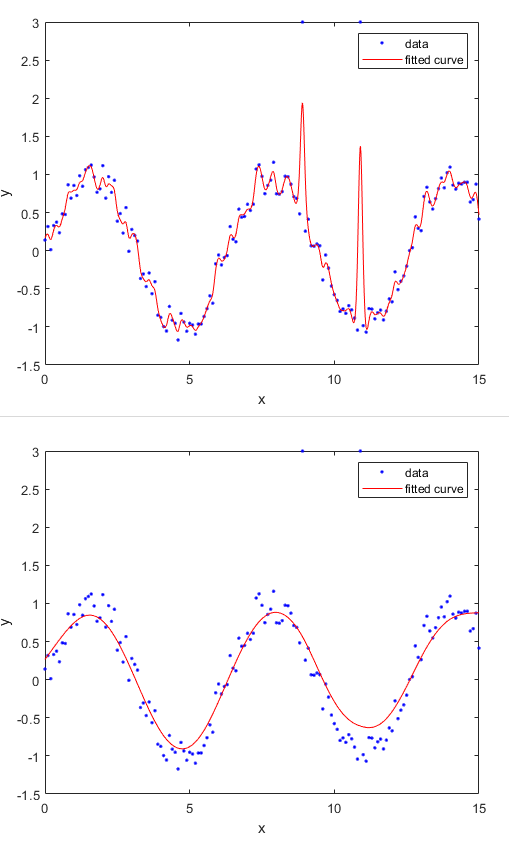
除了对数据进行拟合，MATLAB还支持对数据进行插值

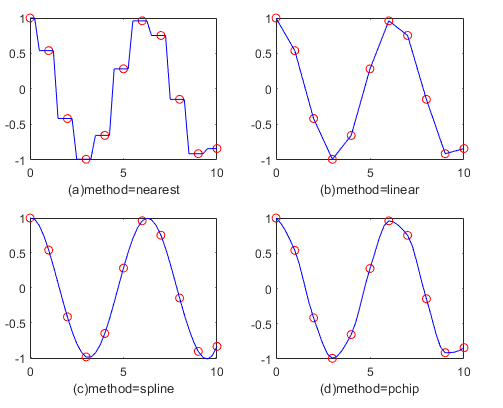
一维数据插值

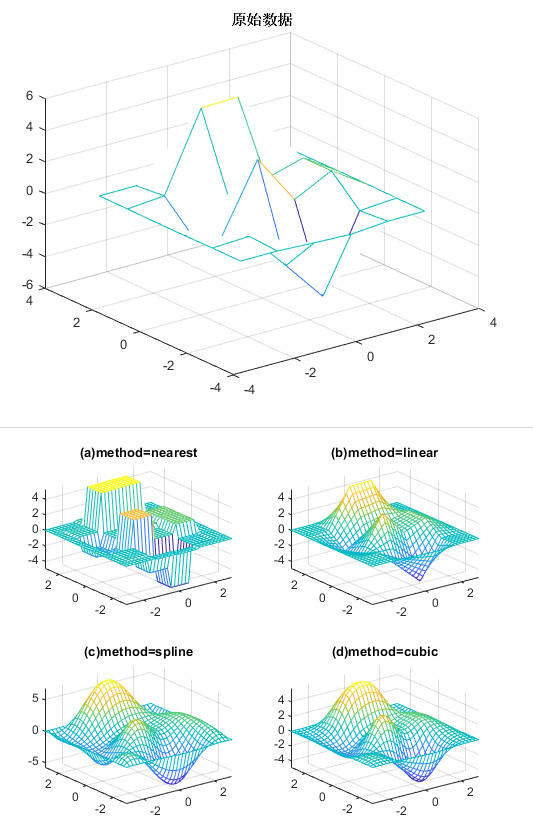
二维数据插值

三维数据插值

使用fit函数进行插值

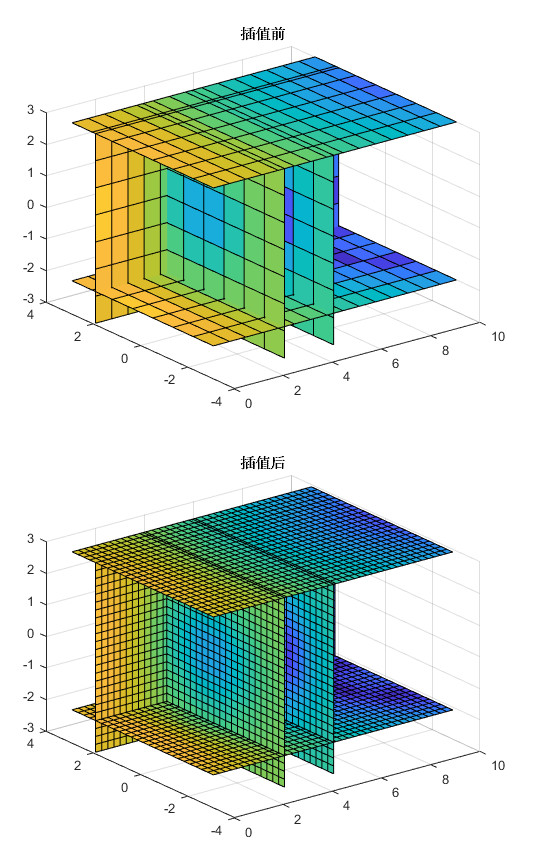
使用fit函数进行插值

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删